Introduction¶
**Code not tidied, but should work OK**
Dataset originaly obtained from https://github.com/suarasaur/dinosaurs
In [1]:
import numpy as np
import matplotlib.pyplot as plt
import pdb
Read and convert data¶
In [2]:
with open('dinosaurs.csv') as f:
data = [x.strip() for x in f.readlines()]
data[:4]
Out[2]:
In [3]:
chars = list(set(''.join(data))) # ['x', 'z', 'j', 'g', ... ]
chars.insert(0, ' ') # use space as not-a-char tag, used for padding
ch2i = {ch:i for i,ch in enumerate(chars)} # {' ': 0, 'x': 1, 'z': 2, 'j': 3, 'g': 4, ... }
i2ch = {i:ch for ch,i in ch2i.items()} # {0: ' ', 1: 'x', 2: 'z', 3: 'j', 4: 'g', ... }
In [4]:
np.random.seed(0)
np.random.shuffle(data)
data[:4]
Out[4]:
In [5]:
max_len = len(max(data, key=len)) # length of longest dino name
for i, dino in enumerate(data):
data[i] = dino.ljust(max_len) # pad all names with spaces to same length
data[:4]
Out[5]:
In [6]:
vocab_size = len(chars)
In [7]:
[ch2i[x] for x in dino]
Out[7]:
In [8]:
indices = np.zeros(shape=[len(data), max_len], dtype=int)
In [9]:
indices
Out[9]:
In [10]:
for i, dino_name in enumerate(data):
indices[i] = [ch2i[x] for x in dino_name]
In [11]:
data[234]
Out[11]:
In [12]:
''.join([i2ch[x] for x in indices[234]])
Out[12]:
In [13]:
onehot = np.zeros(shape=[len(data), max_len, vocab_size], dtype=int)
In [14]:
for i in range(len(indices)):
for j in range(max_len):
onehot[i, j, indices[i,j]] = 1
In [15]:
indices[0, 0]
Out[15]:
In [16]:
onehot[0]
Out[16]:
In [17]:
''.join([i2ch[np.argmax(x)] for x in onehot[234]])
Out[17]:
In [18]:
onehot.shape
Out[18]:
Neural Network¶
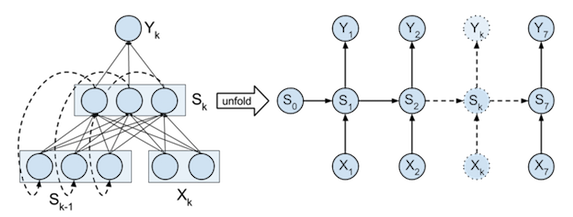
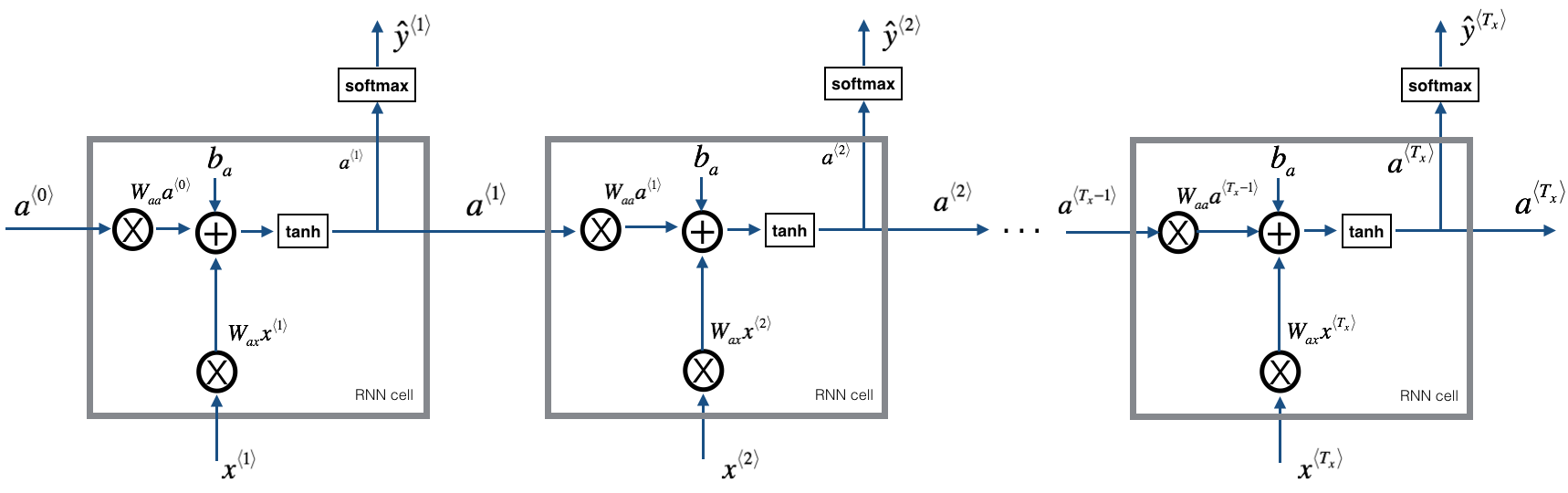
In [19]:
import numpy as np
import matplotlib.pyplot as plt
import pdb
Hyperbolic Tangent
In [21]:
def tanh(x):
return np.tanh(x)
def tanh_der(x):
return 1.0 - np.tanh(x)**2
Softmax
In [22]:
# see e.g. here: https://deepnotes.io/softmax-crossentropy
def softmax(x):
"""Numerically stable softmax"""
max_ = np.max(x, axis=-1, keepdims=True) # shape: (n_batch, 1)
ex = np.exp(x - max_) # shape: (n_batch, n_out)
ex_sum = np.sum(ex, axis=-1, keepdims=True) # shape: (n_batch, 1)
return ex / ex_sum # probabilities shape: (n_batch, n_out)
In [23]:
def cross_entropy(y, y_hat):
"""CE for one-hot targets y, averages over batch."""
assert np.alltrue(y.sum(axis=-1) == 1) # make sure y is one-hot encoded
assert np.alltrue(y.max(axis=-1) == 1)
prob_correct = y_hat[range(len(y_hat)), np.argmax(y, axis=-1)] # pick y_hat for correct class (n_batch,)
return np.average( -np.log(prob_correct) )
In [ ]:
In [24]:
def forward(x, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
x_t = {}
s_t = {}
z_t = {}
s_t[-1] = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
T = x.shape[1]
for t in range(T):
x_t[t] = x[:,t,:]
z_t[t] = s_t[t-1] @ Whh + x_t[t] @ Wxh
s_t[t] = tanh(z_t[t])
z_out = s_t[t] @ Who
y_hat = softmax( z_out )
return y_hat
In [25]:
def backprop(x, y, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
assert y.ndim==2 and y.shape[1:]==(1,)
assert len(x) == len(y)
# Init
x_t = {}
s_t = {}
z_t = {}
s_t[-1] = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
T = x.shape[1]
# Forward
for t in range(T): # t = [0, 1, 2, 3]
x_t[t] = x[:,t,:] # pick time-step input x_[t].shape = (n_batch, n_in)
z_t[t] = s_t[t-1] @ Whh + x_t[t] @ Wxh
s_t[t] = tanh(z_t[t])
z_out = s_t[t] @ Who
y_hat = softmax( z_out )
# Backward
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
ro = y_hat - y # Backprop through loss funt.
dWho = s_t[t].T @ ro #
ro = ro @ Who.T * tanh_der(z_t[t]) # Backprop into hidden state
for t in reversed(range(T)): # t = [3, 2, 1, 0]
dWxh += x_t[t].T @ ro
dWhh += s_t[t-1].T @ ro
if t != 0: # don't backprop into t=-1
ro = ro @ Whh.T * tanh_der(z_t[t-1]) # Backprop into previous time step
return y_hat, dWxh, dWhh, dWho
In [ ]:
def train_rnn(x, y, nb_epochs, learning_rate, Wxh, Whh, Who):
losses = []
for e in range(nb_epochs):
y_hat, dWxh, dWhh, dWho = backward(x, y, Wxh, Whh, Who)
Wxh += -learning_rate * dWxh
Whh += -learning_rate * dWhh
Who += -learning_rate * dWho
# Log and print
loss_train = mse(x, y, Wxh, Whh, Who)
losses.append(loss_train)
if e % (nb_epochs / 10) == 0:
print('loss ', loss_train.round(4))
return losses
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
In [ ]:
Gradient Check¶
In [ ]:
def numerical_gradient(x, y, Wxh, Whh, Who):
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
eps = 1e-4
for r in range(len(Wxh)):
for c in range(Wxh.shape[1]):
Wxh_pls = Wxh.copy()
Wxh_min = Wxh.copy()
Wxh_pls[r, c] += eps
Wxh_min[r, c] -= eps
l_pls = mse(x, y, Wxh_pls, Whh, Who)
l_min = mse(x, y, Wxh_min, Whh, Who)
dWxh[r, c] = (l_pls - l_min) / (2*eps)
for r in range(len(Whh)):
for c in range(Whh.shape[1]):
Whh_pls = Whh.copy()
Whh_min = Whh.copy()
Whh_pls[r, c] += eps
Whh_min[r, c] -= eps
l_pls = mse(x, y, Wxh, Whh_pls, Who)
l_min = mse(x, y, Wxh, Whh_min, Who)
dWhh[r, c] = (l_pls - l_min) / (2*eps)
for r in range(len(Who)):
for c in range(Who.shape[1]):
Who_pls = Who.copy()
Who_min = Who.copy()
Who_pls[r, c] += eps
Who_min[r, c] -= eps
l_pls = mse(x, y, Wxh, Whh, Who_pls)
l_min = mse(x, y, Wxh, Whh, Who_min)
dWho[r, c] = (l_pls - l_min) / (2*eps)
return dWxh, dWhh, dWho
In [ ]: