Introduction¶
This notebooks presents basic Deep Q-Network (DQN) used to solve OpenAI Gym Classic Control environments like Mountain Car, Inverted Pendulum and so on. In this notebook we use DQN without target network for educational purposes. For practical applications use target network.
The environments solved in this notebook are:
- MountainCar-v0 - modified to remove 200 step time limit
- Pendulum-v0 - modified with discrete actions and converted state space
- CartPole-v0
- Acrobot-v1
- LunarLander-v2
I tried to match pre-processing and hyper parameters for all the environments. As the result some hyperparams will differ from optimal. Special note goes to frame skip parameter, which is set to 4 for mountain car and moon lander and omitted otherwise. It can be brought to value 2 for all environments and all of them should still train OK. As for training iterations, I used 25k everywhere with exception of LunarLander (200k). Epsilon decay is also elongated for lunar lander.
Imports¶
Imports
import os
import datetime
import itertools
import collections
import numpy as np
import matplotlib.pyplot as plt
Import OpenAI Gym
import gym
Initialise TensorFlow
import tensorflow as tf
gpu_options = tf.GPUOptions(allow_growth=True) # init TF ...
config=tf.ConfigProto(gpu_options=gpu_options) # w/o taking ...
with tf.Session(config=config): pass # all GPU memory
Import helpers for plotting (source file: helpers.py)
import helpers
import importlib
importlib.reload(helpers);
Q-Learning¶
Epsilon random policy
def policy(st, model, eps):
if np.random.rand() > eps:
q_values = model.eval(np.stack([st]))
return np.argmax(q_values)
else:
return env.action_space.sample()
Main training loop. Supports resuming from pre-trained agent and callbacks.
def q_learning(env, frames, gamma, eps_decay_steps, eps_target,
batch_size, model, mem, start_step=0,
callback=None, trace=None, render=False):
"""Q-Learning, supprots resume
Note: If resuming, all parameters should be identical to original call, with
exception of 'start_step' and 'frames'.
Params:
env - environment
frames - number of time steps to execute
gamma - discount factor [0..1]
eps_decay_steps - decay epsilon-greedy param over that many time steps
eps_target - epsilon-greedy param after decay
batch_size - neural network batch size from memory buffer
model - function approximator, already initialised, with methods:
eval(state, action) -> float
train(state, target) -> None
mem - memory reply buffer
start_step - if continuning, pass in return value (tts_) here
callback - optional callback to execute
trace - this object handles data logging, plotting etc.
render - render openai gym environment?
"""
def eps_schedule(tts, eps_decay_steps, eps_target):
if tts > eps_decay_steps:
return eps_target
else:
eps_per_step_change = (1-eps_target) / eps_decay_steps
return 1.0 - tts * eps_per_step_change
assert len(mem) >= batch_size
tts_ = start_step # total time step
for _ in itertools.count(): # count from 0 to infinity
S = env.reset()
episode_reward = 0 # purely for logging
if render: env.render()
for t_ in itertools.count(): # count from 0 to infinity
eps = eps_schedule(tts_, eps_decay_steps, eps_target)
A = policy(S, model, eps)
S_, R, done, _ = env.step(A)
episode_reward += R
if render: env.render()
mem.append(S, A, R, S_, done)
if callback is not None:
callback(tts_, t_, S, A, R, done, eps, episode_reward, model, mem, trace)
states, actions, rewards, n_states, dones, _ = mem.get_batch(batch_size)
targets = model.eval(n_states)
targets = rewards + gamma * np.max(targets, axis=-1)
targets[dones] = rewards[dones] # return of next-to-terminal state is just R
model.train(states, actions, targets)
S = S_
tts_ += 1
if tts_ >= start_step + frames:
return tts_ # so we can pick up where we left
if done:
break
Stripped down version for evaluation. Does not train agent.
def evaluate(env, model, frames=None, episodes=None, eps=0.0, render=False):
assert frames is not None or episodes is not None
total_reward = 0
tts_ = 0 # total time step
for e_ in itertools.count(): # count from 0 to infinity
if episodes is not None and e_ >= episodes:
return total_reward
S = env.reset()
if render: env.render()
for t_ in itertools.count(): # count from 0 to infinity
A = policy(S, model, eps)
S_, R, done, _ = env.step(A)
total_reward += R
if render: env.render()
S = S_
tts_ += 1
if frames is not None and tts_ >= frames:
return
if done:
break
Stripped down version to pre-fill memory buffer with random policy.
def mem_fill(env, mem, steps=None, episodes=None, render=False):
# Fill memory buffer using random policy
tts_ = 0
for e_ in itertools.count():
if episodes is not None and e_ >= episodes:
return
S = env.reset();
if render: env.render()
for t_ in itertools.count():
A = env.action_space.sample() # random policy
S_, R, done, _ = env.step(A)
if render: env.render()
mem.append(S, A, R, S_, done)
S = S_
tts_ += 1
if steps is not None and tts_ >= steps:
return
if done:
break
Function Approximators and Memory¶
Definition of simple neural network with two hidden layers. As as side note, for classic control tasks tilings work much better.
class TFNeuralNet():
def __init__(self, nb_in, nb_hid_1, nb_hid_2, nb_out, lr):
self.nb_in = nb_in
self.nb_hid_1 = nb_hid_1
self.nb_hid_2 = nb_hid_2
self.nb_out = nb_out
tf.reset_default_graph()
self._x = tf.placeholder(name='xx', shape=[None, nb_in], dtype=tf.float32)
self._y = tf.placeholder(name='yy', shape=[None, nb_out], dtype=tf.float32)
self._h_hid_1 = tf.layers.dense(self._x, units=nb_hid_1,
activation=tf.nn.relu, name='Hidden_1')
self._h_hid_2 = tf.layers.dense(self._h_hid_1, units=nb_hid_2,
activation=tf.nn.relu, name='Hidden_2')
self._y_hat = tf.layers.dense(self._h_hid_2, units=nb_out,
activation=None, name='Output')
self._loss = tf.losses.mean_squared_error(self._y, self._y_hat)
self._optimizer = tf.train.RMSPropOptimizer(learning_rate=lr)
self._train_op = self._optimizer.minimize(self._loss)
self._sess = tf.Session()
self._sess.run(tf.global_variables_initializer())
def backward(self, x, y):
assert x.ndim == y.ndim == 2
_, y_hat, loss = self._sess.run([self._train_op, self._y_hat, self._loss],
feed_dict={self._x: x, self._y:y})
return y_hat, loss
def forward(self, x):
return self._sess.run(self._y_hat, feed_dict={self._x: x})
def save(self, filepath):
saver = tf.train.Saver()
saver.save(self._sess, filepath)
def load(self, filepath):
saver = tf.train.Saver()
saver.restore(self._sess, filepath)
Function approximator wrapper. Mostly performs sanity check and input/output normalisation.
class TFFunctApprox():
def __init__(self, model, st_low, st_high, rew_mean, rew_std, nb_actions):
"""Q-function approximator using Keras model
Args:
model: TFNeuralNet model
"""
st_low = np.array(st_low);
st_high = np.array(st_high)
self._model = model
assert st_low.ndim == 1 and st_low.shape == st_high.shape
if len(st_low) != model.nb_in:
raise ValueError('Input shape does not match state_space shape')
if nb_actions != model.nb_out:
raise ValueError('Output shape does not match action_space shape')
# normalise inputs
self._offsets = st_low + (st_high - st_low) / 2
self._scales = 1 / ((st_high - st_low) / 2)
self._rew_mean = rew_mean
self._rew_std = rew_std
def eval(self, states):
assert isinstance(states, np.ndarray)
assert states.ndim == 2
inputs = (states - self._offsets) * self._scales
y_hat = self._model.forward(inputs)
#return y_hat
return y_hat*self._rew_std + self._rew_mean
def train(self, states, actions, targets):
assert isinstance(states, np.ndarray)
assert isinstance(actions, np.ndarray)
assert isinstance(targets, np.ndarray)
assert states.ndim == 2
assert actions.ndim == 1
assert targets.ndim == 1
assert len(states) == len(actions) == len(targets)
targets = (targets-self._rew_mean) / self._rew_std # normalise
inputs = (states - self._offsets) * self._scales
all_targets = self._model.forward(inputs) # this should normalised already
all_targets[np.arange(len(all_targets)), actions] = targets
self._model.backward(inputs, all_targets)
Memory reply buffer. Reasonably fast impl., doesn't do memory copies when picking batches. This will be useful for Atari. Python deque is very slow.
class Memory:
"""Circular buffer for DQN memory reply. Fairly fast."""
def __init__(self, max_len, state_shape, state_dtype):
"""
Args:
max_len: maximum capacity
"""
assert isinstance(max_len, int)
assert max_len > 0
self.max_len = max_len # maximum length
self._curr_insert_ptr = 0 # index to insert next data sample
self._curr_len = 0 # number of currently stored elements
state_arr_shape = [max_len] + list(state_shape)
self._hist_St = np.zeros(state_arr_shape, dtype=state_dtype)
self._hist_At = np.zeros(max_len, dtype=int)
self._hist_Rt_1 = np.zeros(max_len, dtype=float)
self._hist_St_1 = np.zeros(state_arr_shape, dtype=state_dtype)
self._hist_done_1 = np.zeros(max_len, dtype=bool)
def append(self, St, At, Rt_1, St_1, done_1):
"""Add one sample to memory, override oldest if max_len reached.
Args:
St [np.ndarray] - state
At [int] - action
Rt_1 [float] - reward
St_1 [np.ndarray] - next state
done_1 [bool] - next state terminal?
"""
self._hist_St[self._curr_insert_ptr] = St
self._hist_At[self._curr_insert_ptr] = At
self._hist_Rt_1[self._curr_insert_ptr] = Rt_1
self._hist_St_1[self._curr_insert_ptr] = St_1
self._hist_done_1[self._curr_insert_ptr] = done_1
if self._curr_len < self.max_len: # keep track of current length
self._curr_len += 1
self._curr_insert_ptr += 1 # increment insertion pointer
if self._curr_insert_ptr >= self.max_len: # roll to zero if needed
self._curr_insert_ptr = 0
def __len__(self):
"""Number of samples in memory, 0 <= length <= max_len"""
return self._curr_len
def get_batch(self, batch_len):
"""Sample batch of data, with repetition
Args:
batch_len: nb of samples to pick
Returns:
states, actions, rewards, next_states, next_done, indices
Each returned element is np.ndarray with length == batch_len
"""
assert self._curr_len > 0
assert batch_len > 0
indices = np.random.randint( # randint much faster than np.random.sample
low=0, high=self._curr_len, size=batch_len, dtype=int)
states = np.take(self._hist_St, indices, axis=0)
actions = np.take(self._hist_At, indices, axis=0)
rewards_1 = np.take(self._hist_Rt_1, indices, axis=0)
states_1 = np.take(self._hist_St_1, indices, axis=0)
dones_1 = np.take(self._hist_done_1, indices, axis=0)
return states, actions, rewards_1, states_1, dones_1, indices
def pick_last(self, nb):
"""Pick last nb elements from memory
Returns:
states, actions, rewards, next_states, done_1, indices
Each returned element is np.ndarray with length == batch_len
"""
assert nb <= self._curr_len
start = self._curr_insert_ptr - nb # inclusive
end = self._curr_insert_ptr # not inclusive
indices = np.array(range(start,end), dtype=int) # indices to pick, can be neg.
indices[indices < 0] += self._curr_len # loop negative to positive
states = np.take(self._hist_St, indices, axis=0)
actions = np.take(self._hist_At, indices, axis=0)
rewards_1 = np.take(self._hist_Rt_1, indices, axis=0)
states_1 = np.take(self._hist_St_1, indices, axis=0)
dones_1 = np.take(self._hist_done_1, indices, axis=0)
return states, actions, rewards_1, states_1, dones_1, indices
Experiment Setup¶
Environment wrapper to skip frames. Also known as action repeat. Really helps with some environments, e.g. mountain car.
class WrapFrameSkip():
def __init__(self, env, frameskip):
assert frameskip >= 1
self._env = env
self._frameskip = frameskip
self.observation_space = env.observation_space
self.action_space = env.action_space
def reset(self):
return self._env.reset()
def step(self, action):
sum_rew = 0
for _ in range(self._frameskip):
obs, rew, done, info = self._env.step(action)
sum_rew += rew
if done: break
return obs, sum_rew, done, info
def render(self, mode='human'):
return self._env.render(mode=mode)
def close(self):
self._env.close()
This object is a basic data logger. If you don't want to generate plots, you can mostly ignore it
class Trace():
def __init__(self, eval_every, render=False, test_states=None, state_labels=None):
if test_states is not None:
assert test_states.ndim == 2
self.enable_plotting = False
self.eval_every = eval_every
self.test_states = test_states
self.state_labels = state_labels
self.tstep = 0
self.total_tstep = 0
self.q_values = collections.OrderedDict()
self.ep_rewards = collections.defaultdict(float)
self.last_ep_reward = None
self.states = []
self.actions = []
self.rewards = [] # t+1
self.dones = [] # t+1
self.epsilons = []
Callback which is called every single training iteration, it does as follows:
- fill up trace object with basic logging data
- print training progress
- perform evaluation of
test_states - optionally plot agent state
def callback(total_time_step, tstep, st, act, rew_, done_,
eps, ep_reward, model, memory, trace):
"""Called from gradient_MC after every episode.
Params:
episode [int] - episode number
tstep [int] - timestep within episode
model [obj] - function approximator
trace [list] - list to write results to"""
assert total_time_step == trace.total_tstep
trace.tstep = tstep
trace.states.append(st)
trace.actions.append(act)
trace.rewards.append(rew_)
trace.dones.append(done_)
trace.epsilons.append(eps)
if done_:
trace.ep_rewards[total_time_step] = ep_reward
trace.last_ep_reward = ep_reward
#
# Print, Evaluate, Plot
#
if (trace.eval_every is not None) and (trace.total_tstep % trace.eval_every == 0):
last_ep_rew = trace.last_ep_reward
reward_str = str(round(last_ep_rew, 3)) if last_ep_rew is not None else 'None'
print(f'wall: {datetime.datetime.now().strftime("%H:%M:%S")} '
f'ep: {len(trace.ep_rewards):3} tstep: {tstep:4} '
f'total tstep: {trace.total_tstep:6} '
f'eps: {eps:5.3f} reward: {reward_str} ')
if len(st) == 2:
# We are working with 2D environment,
# eval. Q-Value function across whole state space
q_arr = helpers.eval_state_action_space(model, env, split=[128,128])
trace.q_values[trace.total_tstep] = q_arr
else:
# Environment is not 2D,
# eval. on pre-defined random sample of states
if trace.test_states is not None:
y_hat = model.eval(trace.test_states)
trace.q_values[trace.total_tstep] = y_hat
if trace.enable_plotting:
helpers.plot_all(env, model, memory, trace)
print('■'*80)
trace.total_tstep += 1
MountainCar¶
Start with mountain car environment
Notes:
- OpenAI gym imposes 200 step limit, which makes this environment extremely hard to solve with DQN - we remove this limit
- Frame-skip (aka action repeat) is technically not necessary, but makes training much easier, good value is frameskip=4
The nut and bolt of mountain car is that agent gets extremely sparse reward on successful exit. Shortest possible exit trajectory is approx 120-130 steps. If we impose 200 step limit and don't repeat actions this means agent has to perform series of 120-130 actions exactly correctly in the row with very little margin for error. If agent doesn't succeed it gets reset back to beginning on step 200. To do this with random exploratory policy is virtually impossible.
Note that this can still be solved easily with linear function approximation (local updates) and optimistic initialisation which facilitates continuing exploration. This is not possible with DQN.
def experiment_mountaincar():
neural_net = TFNeuralNet(nb_in=2, nb_hid_1=64, nb_hid_2=64, nb_out=3, lr=0.00025)
model = TFFunctApprox(neural_net,
env.observation_space.low,
env.observation_space.high,
rew_mean=-50,
rew_std=15,
nb_actions=env.action_space.n)
mem = Memory(max_len=100000, state_shape=(2,), state_dtype=float)
mem_fill(env, mem, steps=10000)
test_states, _, _, _, _, _ = mem.get_batch(10)
trace = Trace(eval_every=1000, test_states=test_states)
return trace, model, mem
Setup the experiment
env = gym.make('MountainCar-v0').env # remove 200 step limit
env = WrapFrameSkip(env, frameskip=4)
trace, model, mem = experiment_mountaincar()
# trace.enable_plotting = True
Train the agent
tts = q_learning(env, frames=25000, gamma=.99,
eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
model=model, mem=mem, callback=callback, trace=trace)
Optional: train some more
# tts = q_learning(env, frames=5000, gamma=.99,
# eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
# model=model, mem=mem, start_step=tts, callback=callback, trace=trace)
Optional: plot the agent state
# helpers.plot_all(env, model, mem, trace, print_=True)
Save weights
model._model.save('./tf_models/MountainCar.ckpt')
Load weights
model._model.load('./tf_models/MountainCar.ckpt')
Enjoy trained agent
# In Jupyter, press squre '■' in top menu to quit animation
try: evaluate(env, model, frames=float('inf'), eps=0.0, render=True)
except KeyboardInterrupt: pass
finally: env.close()
Result
Expected agent behaviour after 15000 iterations

If you enable plotting, then output after training should be in roughly as follows
wall: 16:45:30 ep: 91 tstep: 22 total tstep: 15000 eps: 0.325 reward: -134.0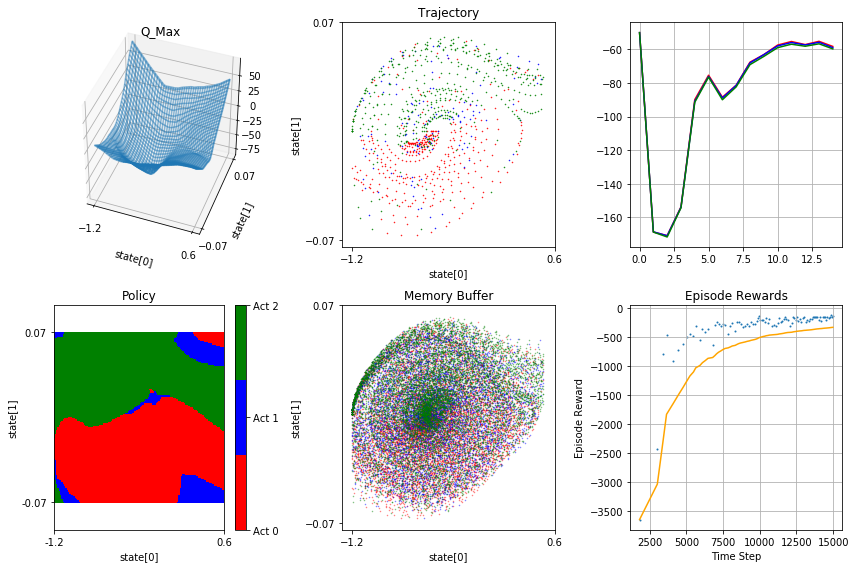
Where:
- Q_Max - is a plot of q-function max over possible actions
- Trajectory - is top-down view of agent trajectory. Agent starts roughly in the centre and exits to the right. Colour indicates action, see policy plot
- Q Values - is a plot of average q-values for set or randomly selected states - this shows how q-values develop during training
- Policy - is a top-down plot of agent policy. Green is accelerate right, red is accelerate left, blue is neutral
- Memory Buffer - is a snapshot of memory buffer, same format as Trajectory plot
- Episode Rewards - individual rewards acquired (blue dots) and running average (yellow) over the training period
Pendulum¶
Pendulum is in my opinion actually quite a bit easier than mountain car. Mainly because of rich reward signal.
Notes:
- OpenAI pendulum has continuous actions while basic DQN requires discrete actions - we will discretise it
- by default state space is 3-vector: [cos(angle), sin(angle), velocity] - to be able to plot whole state space we reduce it to [angle, velocity]
class Pendulum2DEnv():
def __init__(self):
self._env = gym.make('Pendulum-v0')
self.observation_space = gym.spaces.Box(
low=np.array([-np.pi, -8.0]), high=np.array([np.pi, 8.0]), dtype=np.float32 )
self.action_space = gym.spaces.Discrete(n=3)
def reset(self):
cos, sin, vel = self._env.reset()
theta = np.arctan2(sin, cos)
return np.array([theta, vel])
def step(self, action):
torques = [-2.0, 0.0, 2.0]
# torques = [-2.0, -.5, 0.0, .5, 2.0]
joint_effort = torques[action]
obs, rew, done, _ = self._env.step([joint_effort])
cos, sin, vel = obs
theta = np.arctan2(sin, cos)
return np.array([theta, vel]), rew, done, obs
def render(self, mode='human'):
return self._env.render(mode=mode)
def close(self):
self._env.close()
def experiment_pendulum():
neural_net = TFNeuralNet(nb_in=2, nb_hid_1=64, nb_hid_2=64, nb_out=3, lr=0.00025)
model = TFFunctApprox(neural_net,
env.observation_space.low,
env.observation_space.high,
rew_mean=-210,
rew_std=50,
nb_actions=env.action_space.n)
mem = Memory(max_len=100000, state_shape=(2,), state_dtype=float)
mem_fill(env, mem, steps=10000)
test_states, _, _, _, _, _ = mem.get_batch(10)
trace = Trace(eval_every=1000, test_states=test_states)
return trace, model, mem
Setup the experiment
env = Pendulum2DEnv()
trace, model, mem = experiment_pendulum()
# trace.enable_plotting = True
Train the agent
tts = q_learning(env, frames=25000, gamma=.99,
eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
model=model, mem=mem, callback=callback, trace=trace)
Optional: train some more
# tts = q_learning(env, frames=5000, gamma=.99,
# eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
# model=model, mem=mem, start_step=tts, callback=callback, trace=trace)
Optional: plot the agent state
# helpers.plot_all(env, model, mem, trace, print_=True)
Save weights
model._model.save('./tf_models/Pendulum.ckpt')
Load weights
model._model.load('./tf_models/Pendulum.ckpt')
Enjoy trained agent
# In Jupyter, press squre '■' in top menu to quit animation
try: evaluate(env, model, frames=float('inf'), eps=0.0, render=True)
except KeyboardInterrupt: pass
finally: env.close()
Result
Expected agent behaviour after 25000 iterations
If you enable plotting, then output after training should be in roughly as follows
wall: 08:13:49 ep: 250 tstep: 99 total tstep: 25000 eps: 0.100 reward: -227.530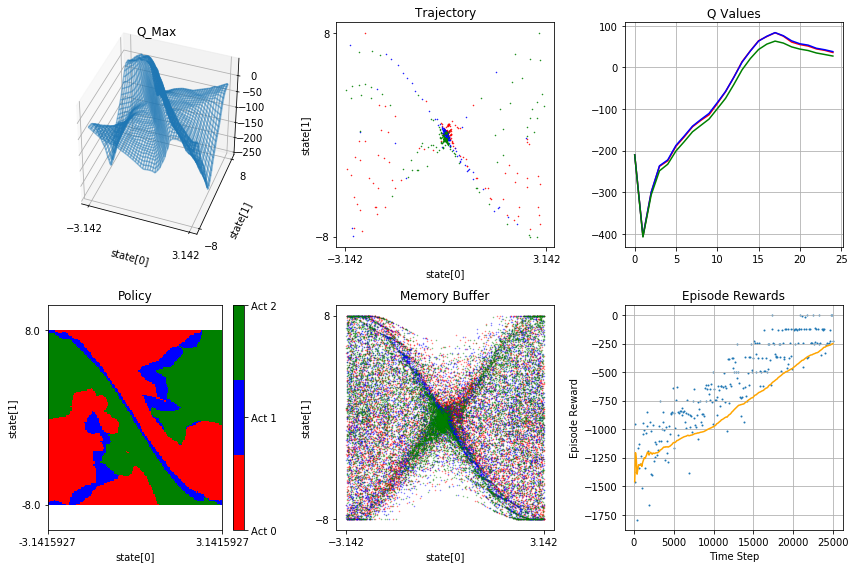
Where:
- Q_Max - is a plot of q-function max over possible actions
- Trajectory - is top-down view of agent trajectory. Agent starts roughly in the centre and exits to the right. Colour indicates action, see policy plot
- Q Values - is a plot of average q-values for set or randomly selected states - this shows how q-values develop during training
- Policy - is a top-down plot of agent policy. Green is accelerate right, red is accelerate left, blue is neutral
- Memory Buffer - is a snapshot of memory buffer, same format as Trajectory plot
- Episode Rewards - individual rewards acquired (blue dots) and running average (yellow) over the training period
Cartpole¶
Everybody loves cartpole!
Notes:
- this environment no longer has 2d state space so we can't plot it all :( - as a result plots look differently
This environment has peculiar dynamic where positive reward, along with non-corrected maximisation bias in Q-Function (we don't use Dual-DQN) causes runaway Q-Value effect where Q-Values increase continuously. This is ok for now, because RELATIVE Q-Values are still good enough to select correct action. I think using target network along with Dual-DQN would help with this problem.
def experiment_cartpole():
neural_net = TFNeuralNet(nb_in=4, nb_hid_1=64, nb_hid_2=64, nb_out=2, lr=0.00025)
model = TFFunctApprox(neural_net,
st_low=np.array([-.2, -1.0, -0.15, -1.0]),
st_high=np.array([.2, 1.0, 0.15, 1.0]),
rew_mean=0,
rew_std=1,
nb_actions=env.action_space.n)
mem = Memory(max_len=100000, state_shape=(4,), state_dtype=float)
mem_fill(env, mem, steps=10000)
test_states, _, _, _, _, _ = mem.get_batch(10)
trace = Trace(eval_every=1000, test_states=test_states)
return trace, model, mem
Setup the experiment
env = env = gym.make('CartPole-v0')
trace, model, mem = experiment_cartpole()
# trace.enable_plotting = True
Train the agent
tts = q_learning(env, frames=25000, gamma=.99,
eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
model=model, mem=mem, callback=callback, trace=trace)
Optional: train some more
# tts = q_learning(env, frames=5000, gamma=.99,
# eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
# model=model, mem=mem, start_step=tts, callback=callback, trace=trace)
Optional: plot the agent state
# helpers.plot_all(env, model, mem, trace, print_=True)
Save weights
model._model.save('./tf_models/CartPole.ckpt')
Load weights
model._model.load('./tf_models/CartPole.ckpt')
Enjoy trained agent
# In Jupyter, press squre '■' in top menu to quit animation
try: evaluate(env, model, frames=float('inf'), eps=0.0, render=True)
except KeyboardInterrupt: pass
finally: env.close()
Result
Expected agent behaviour after 25000 iterations
If you enable plotting, then output after training should be in roughly as follows
wall: 10:16:24 ep: 349 tstep: 125 total tstep: 24000 eps: 0.100 reward: 200.0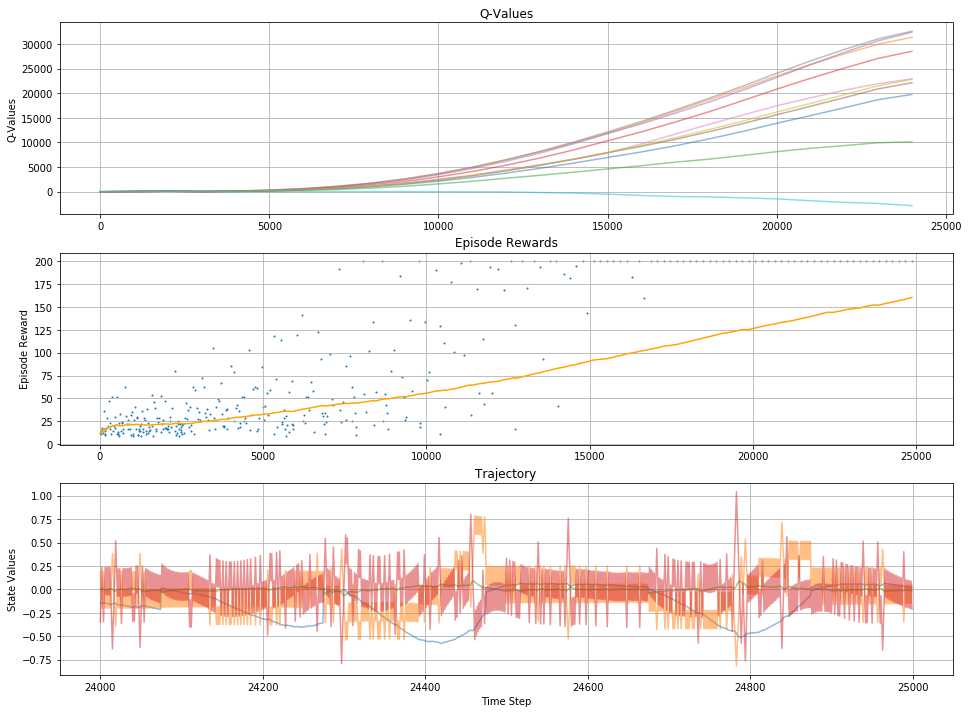
Where:
- Q Values - is a plot of average q-values for set of states - this shows how q-values develop during training
- Episode Rewards - individual rewards acquired (blue dots) and running average (yellow) over the training period
- Trajectory - is set of state variables over time within one or more episodes
Acrobot¶
This is a variation of pendulum environment
def experiment_acrobot():
neural_net = TFNeuralNet(nb_in=6, nb_hid_1=64, nb_hid_2=64, nb_out=3, lr=0.00025)
model = TFFunctApprox(neural_net,
env.observation_space.low,
env.observation_space.high,
rew_mean=-70,
rew_std=10,
nb_actions=env.action_space.n)
mem = Memory(max_len=100000, state_shape=(6,), state_dtype=float)
mem_fill(env, mem, steps=10000)
test_states, _, _, _, _, _ = mem.get_batch(10)
trace = Trace(eval_every=1000, test_states=test_states)
return trace, model, mem
Setup the experiment
env = env = gym.make('Acrobot-v1')
trace, model, mem = experiment_acrobot()
# trace.enable_plotting = True
Train the agent
tts = q_learning(env, frames=25000, gamma=.99,
eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
model=model, mem=mem, callback=callback, trace=trace)
Optional: train some more
# tts = q_learning(env, frames=5000, gamma=.99,
# eps_decay_steps=20000, eps_target=0.1, batch_size=4096,
# model=model, mem=mem, start_step=tts, callback=callback, trace=trace)
Optional: plot the agent state
# helpers.plot_all(env, model, mem, trace, print_=True)
Save weights
model._model.save('./tf_models/Acrobot.ckpt')
Load weights
model._model.load('./tf_models/Acrobot.ckpt')
Enjoy trained agent
# In Jupyter, press squre '■' in top menu to quit animation
try: evaluate(env, model, frames=float('inf'), eps=0.0, render=True)
except KeyboardInterrupt: pass
finally: env.close()
Result
Expected agent behaviour after 25000 iterations

If you enable plotting, then output after training should be in roughly as follows
wall: 09:23:11 ep: 332 tstep: 31 total tstep: 24000 eps: 0.100 reward: -90.0
Where:
- Q Values - is a plot of average q-values for set of states - this shows how q-values develop during training
- Episode Rewards - individual rewards acquired (blue dots) and running average (yellow) over the training period
- Trajectory - is set of state variables over time within one or more episodes
Lunar Lander¶
def experiment_lunarlander():
neural_net = TFNeuralNet(nb_in=8, nb_hid_1=64, nb_hid_2=64, nb_out=4, lr=0.00025)
model = TFFunctApprox(neural_net,
st_low=np.array([-1., -1., -1., -1., -1., -1., -1., -1.]),
st_high=np.array([ 1., 1., 1., 1., 1., 1., 1., 1.]),
rew_mean=0,
rew_std=1,
nb_actions=env.action_space.n)
mem = Memory(max_len=100000, state_shape=(8,), state_dtype=float)
mem_fill(env, mem, steps=10000)
trace = Trace(eval_every=1000,
test_states=np.array([[0, 1.4, 0, 0, 0, 0, 0, 0], # init
[0, 0.7, 0, 0, 0, 0, 0, 0], # half way
[0, 0.0, 0, 0, 0, 0, 0, 0],]), # landing pad
state_labels=['Pos.x', 'Pos.y', 'Vel.x', 'Vel.y',
'Angle', 'Ang. Vel', 'Left Leg', 'Right Leg'])
return trace, model, mem
Setup the experiment
env = gym.make('LunarLander-v2')
#env = WrapFrameSkip(env, frameskip=4)
trace, model, mem = experiment_lunarlander()
# trace.enable_plotting = True
Train the agent
tts = q_learning(env, frames=200000, gamma=.99,
eps_decay_steps=50000, eps_target=0.1, batch_size=4096,
model=model, mem=mem, callback=callback, trace=trace)
Optional: train some more
# tts = q_learning(env, frames=5000, gamma=.99,
# eps_decay_steps=50000, eps_target=0.1, batch_size=4096,
# model=model, mem=mem, start_step=tts, callback=callback, trace=trace)
Optional: plot the agent state
# helpers.plot_all(env, model, mem, trace, print_=True)
Save weights
model._model.save('./tf_models/LunarLander.ckpt')
Load weights
model._model.load('./tf_models/LunarLander.ckpt')
Enjoy trained agent
# In Jupyter, press squre '■' in top menu to quit animation
try: evaluate(env, model, frames=float('inf'), eps=0.0, render=True)
except KeyboardInterrupt: pass
finally: env.close()
Result
Expected agent behaviour after 25000 iterations
If you enable plotting, then output after training should be in roughly as follows

Where:
- Q Values - is a plot of average q-values for set of states - this shows how q-values develop during training
- Episode Rewards - individual rewards acquired (blue dots) and running average (yellow) over the training period
- Trajectory - is set of state variables over time within one or more episodes
Render HTML5 Video¶
This section is for rendering the animations, ignore
import time
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
def frames_render(env, frames, episodes, eps, model, callback=None, trace=None, render=True, sleep=0):
rendered_frames = []
def policy(st, model, eps):
if np.random.rand() > eps:
stack = np.stack([st]) # convert lazyframe to nn input shape [1, 84, 84, 4]
q_values = model.eval(stack)
return np.argmax(q_values)
else:
return env.action_space.sample()
total_reward = 0
tts_ = 0 # total time step
for e_ in itertools.count(): # count from 0 to infinity
S = env.reset()
if render:
rendered_frames.append(env.render(mode='rgb_array'))
#env.render()
time.sleep(sleep)
for t_ in itertools.count(): # count from 0 to infinity
# print(e_, t_)
A = policy(S, model, eps)
S_, R, done, info = env.step(A)
#total_reward += info['full-reward']
if render:
rendered_frames.append(env.render(mode='rgb_array'))
#env.render()
time.sleep(sleep)
if callback is not None:
callback(tts_, e_, t_, S, A, R, done, eps, model, None, trace)
if done:
break
if frames is not None and tts_ >= frames:
return rendered_frames, total_reward
S = S_
tts_ += 1
if episodes is not None and e_ >= episodes-1:
return rendered_frames, total_reward
env.close()
evaluate(env, frames=None, episodes=1, eps=0.05, model=model, render=True)
rendered_frames, total_reward = frames_render(env, frames=None, episodes=1, eps=0.05, model=model, render=True)
plt.ioff()
fig = plt.figure(figsize=(rendered_frames[0].shape[1] / 72.0,
rendered_frames[0].shape[0] / 72.0), dpi = 72)
ax = fig.add_subplot(111);
patch = ax.imshow(rendered_frames[0])
plt.tick_params(axis='both', which='both', bottom=False, top=False, left=False,
right=False, labelbottom=False, labelleft=False)
def animate(i):
patch.set_data(rendered_frames[i])
anim = animation.FuncAnimation(fig, animate, frames=len(rendered_frames), interval=20, repeat=True)
HTML(anim.to_html5_video())
Then:
- r-click and download html5 video (will save as mp4)
- convert to gif with: https://ezgif.com/video-to-gif