$$ \huge{\underline{\textbf{ First Visit MC Prediction }}} $$

In [1]:
def first_visit_MC_prediction(env, policy, ep, gamma):
"""First Visit MC Prediction
Params:
env - environment
policy - function in a form: policy(state)->action
ep - number of episodes to run
gamma - discount factor
"""
V = dict()
Returns = defaultdict(list) # dict of lists
for _ in range(ep):
traj, T = generate_episode(env, policy)
G = 0
for t in range(T-1,-1,-1):
St, _, _, _ = traj[t] # (st, rew, done, act)
_, Rt_1, _, _ = traj[t+1]
G = gamma * G + Rt_1
if not St in [traj[i][0] for i in range(0, t)]:
Returns[St].append(G)
V[St] = np.average(Returns[St])
return V
Helper functions:
In [2]:
def generate_episode(env, policy):
"""Generete one complete episode.
Returns:
trajectory: list of tuples [(st, rew, done, act), (...), (...)],
where St can be e.g tuple of ints or anything really
T: index of terminal state, NOT length of trajectory
"""
trajectory = []
done = True
while True:
# === time step starts here ===
if done: St, Rt, done = env.reset(), None, False
else: St, Rt, done, _ = env.step(At)
At = policy(St)
trajectory.append((St, Rt, done, At))
if done: break
# === time step ends here ===
return trajectory, len(trajectory)-1
 |
Alternative Implementation¶
Slightly more "sane" in my opinion.
In [3]:
def first_visit_MC_prediction_2(env, policy, ep, gamma):
V = dict()
Counts = defaultdict(float) # Change #1: count number of visits
Returns = defaultdict(float) # Change #2: this stores SUM of Returns
for _ in range(ep):
traj, T = generate_episode(env, policy)
G = 0
for t in range(T-1,-1,-1):
St, _, _, _ = traj[t] # (st, rew, done, act)
_, Rt_1, _, _ = traj[t+1]
G = gamma * G + Rt_1
if not St in [traj[i][0] for i in range(0, t)]:
Counts[St] += 1
Returns[St] += G
# Change #3: do this only once
for state, returns in Returns.items():
V[state] = returns / Counts[state]
return V
Solve Blackjack¶
In [4]:
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
from mpl_toolkits.mplot3d import axes3d
import gym
Create environment
In [5]:
env = gym.make('Blackjack-v0')
Policy function
In [6]:
def policy(St):
p_sum, d_card, p_ace = St
if p_sum >= 20:
return 0 # stick
else:
return 1 # hit
Ploting
In [7]:
def convert_to_arr(V_dict, has_ace):
V_dict = defaultdict(float, V_dict) # assume zero if no key
V_arr = np.zeros([10, 10]) # Need zero-indexed array for plotting
# convert player sum from 12-21 to 0-9
# convert dealer card from 1-10 to 0-9
for ps in range(12, 22):
for dc in range(1, 11):
V_arr[ps-12, dc-1] = V_dict[(ps, dc, has_ace)]
return V_arr
def plot_3d_wireframe(axis, V_dict, has_ace):
Z = convert_to_arr(V_dict, has_ace)
dealer_card = list(range(1, 11))
player_points = list(range(12, 22))
X, Y = np.meshgrid(dealer_card, player_points)
axis.plot_wireframe(X, Y, Z)
def plot_blackjack(V_dict):
fig = plt.figure(figsize=[16,3])
ax_no_ace = fig.add_subplot(121, projection='3d', title='No Ace')
ax_has_ace = fig.add_subplot(122, projection='3d', title='With Ace')
ax_no_ace.set_xlabel('Dealer Showing'); ax_no_ace.set_ylabel('Player Sum')
ax_has_ace.set_xlabel('Dealer Showing'); ax_has_ace.set_ylabel('Player Sum')
plot_3d_wireframe(ax_no_ace, V_dict, has_ace=False)
plot_3d_wireframe(ax_has_ace, V_dict, has_ace=True)
plt.show()
Solve
In [8]:
V = first_visit_MC_prediction(env, policy, ep=20000, gamma=1.0)
plot_blackjack(V)
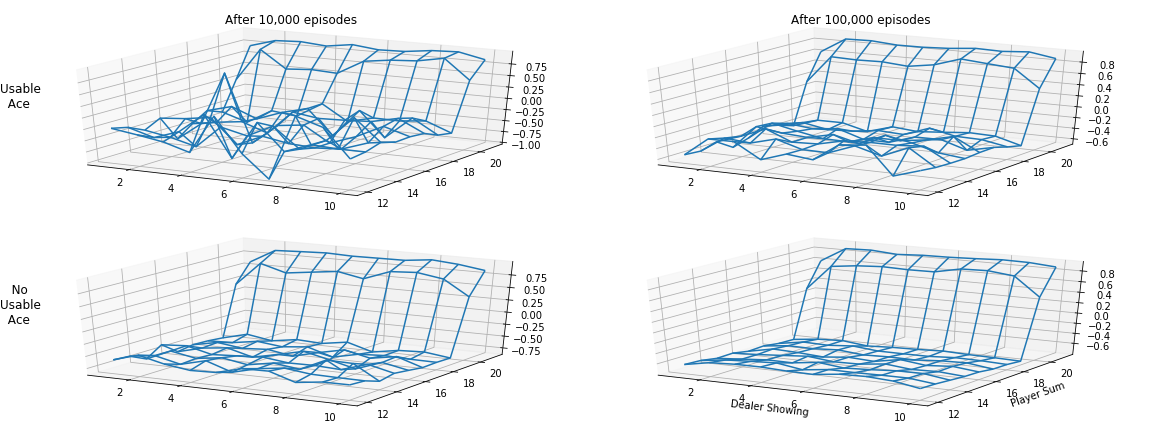
Recreate Figure 5.1¶
In [9]:
V_10k = first_visit_MC_prediction(env, policy, ep=10000, gamma=1.0)
V_100k = first_visit_MC_prediction(env, policy, ep=100000, gamma=1.0)
fig = plt.figure(figsize=[16,6])
ax_10k_no_ace = fig.add_subplot(223, projection='3d')
ax_10k_has_ace = fig.add_subplot(221, projection='3d', title='After 10,000 episodes')
ax_100k_no_ace = fig.add_subplot(224, projection='3d')
ax_100k_has_ace = fig.add_subplot(222, projection='3d', title='After 100,000 episodes')
fig.text(0., 0.75, 'Usable\n Ace', fontsize=12)
fig.text(0., 0.25, ' No\nUsable\n Ace', fontsize=12)
ax_100k_no_ace.set_xlabel('Dealer Showing'); ax_100k_no_ace.set_ylabel('Player Sum')
plot_3d_wireframe(ax_10k_no_ace, V_10k, has_ace=False)
plot_3d_wireframe(ax_10k_has_ace, V_10k, has_ace=True)
plot_3d_wireframe(ax_100k_no_ace, V_100k, has_ace=False)
plot_3d_wireframe(ax_100k_has_ace, V_100k, has_ace=True)
plt.tight_layout()
plt.savefig('assets/fig_0501.png')
plt.show()
Timing Test¶
In [10]:
%timeit first_visit_MC_prediction(env, policy, ep=20000, gamma=1.0)
%timeit first_visit_MC_prediction_2(env, policy, ep=20000, gamma=1.0)