$$ \huge{\underline{\textbf{ Monte Carlo ES Control }}} $$

In [1]:
def monte_carlo_ES_control(env, ep, gamma):
"""Monte Carlo ES Control
Params:
env - environment
ep - number of episodes to run
gamma - discount factor
"""
pi = defaultdict(int) # default action: 0
Q = defaultdict(float) # default Q value: 0
Returns = defaultdict(list) # dict of lists
for _ in range(ep):
S0, A0 = env.sample_state_action()
traj, T = generate_episode_ES(env, pi, S0, A0)
G = 0
for t in range(T-1,-1,-1):
St, _, _, At = traj[t] # (st, rew, done, act)
_, Rt_1, _, _ = traj[t+1]
G = gamma * G + Rt_1
if not (St, At) in [(traj[i][0], traj[i][3]) for i in range(0, t)]:
Returns[(St, At)].append(G)
Q[(St, At)] = np.average(Returns[(St, At)])
pi[St] = np.argmax([Q[St,a] for a in range(env.nb_actions)])
return Q, pi
Helper functions:
In [2]:
def generate_episode_ES(env, pi, S0, A0):
"""Generete one complete episode.
Returns:
trajectory: list of tuples [(st, rew, done, act), (...), (...)],
where St can be e.g tuple of ints or anything really
T: index of terminal state, NOT length of trajectory
"""
trajectory = []
done = True
while True:
# === time step starts here ===
if done:
St, Rt, done = env.reset_es(S0), None, False
At = A0
else:
St, Rt, done, _ = env.step(At)
At = pi[St]
trajectory.append((St, Rt, done, At))
if done: break
# === time step ends here ===
return trajectory, len(trajectory)-1
 |
Solve Blackjack¶
In [3]:
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
from mpl_toolkits.mplot3d import axes3d
import gym
Extend OpenAI Gym Blackjack-v0 to allow exploring starts
In [4]:
class BlackjackES():
def __init__(self):
self._env = gym.make('Blackjack-v0')
self.nb_actions = 2
def sample_state_action(self):
"""Sample and return valid state & action for exp. starts"""
player_sum = np.random.randint(12, 22)
dealer_shows = np.random.randint(1, 11)
has_ace = np.random.randint(0, 2)
state = (player_sum, dealer_shows, bool(has_ace))
action = np.random.randint(0, 2)
return state, action
def reset_es(self, init_state):
"""Start game from given state"""
player_sum, dealer_shows, has_ace = init_state
assert player_sum in range(12, 22)
assert dealer_shows in range(1, 11)
assert isinstance(has_ace, bool)
self._env.reset() # reset OpenAI env
# draw second card for the dealer
# according to original probabilities
dealer_hides = np.random.choice([1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 10, 10, 10])
# override dealer hand
self._env.dealer = [dealer_shows, dealer_hides]
# pick cards for player to match player_sum and has_ace
if has_ace:
player_hand = [player_sum-11, 1]
else:
if player_sum == 21: player_hand = [10, 9, 2]
else: player_hand = [player_sum-10, 10]
# override player hand
self._env.player = player_hand
# force re-evaluate observation with new hands
obs = self._env._get_obs()
assert obs == init_state
return obs
def step(self, action):
return self._env.step(action)
Create environment
In [5]:
env = BlackjackES()
Ploting
In [6]:
from helpers_0503 import plot_blackjack
Solve Blackjack
- result is only a quick approximation, very unlikely to match the book figure 5.2 exactly
- but with (many) more samples, this will converge to same policy as in the book
In [7]:
Q, pi = monte_carlo_ES_control(env, ep=250000, gamma=1.0) # approx 1 min to run
In [8]:
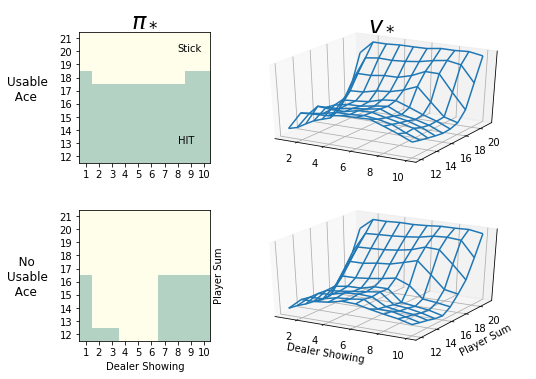
plot_blackjack(Q, pi)
Recreate Figure 5.2¶
In blackjack as presented in the book some states are very difficult to evaluate correctly, because Q-values for hit and stick is almost identical. It takes huge amount of samples to evaluate these states correctly.
First, we will have to modify original algorithm slightly, changes include:
- new parameters:
- add callback parameter - user function called every training episode
- add resume_dicts param - this is so we can pick up training from where we left
- add focus_S0 param - this overrides random initial state selection with single state
- Returns now stores sum of Q-Values, not list of all Q-Values - important speed improvement for longer runs!
- C dict stores number of vistis for each state
- We skip step to check if this is first-visit to state St - this effectively changes algorithm to Every-Visit MC.
In [9]:
def monte_carlo_ES_control_ext(env, ep, gamma, callback=None, resume_dicts=None, focus_S0=None):
"""Monte Carlo ES Control
Params:
env - environment
ep - number of episodes to run
gamma - discount factor
"""
if resume_dicts is None:
pi = defaultdict(int) # this is same as before
C = defaultdict(int) # Change! count number of visits!
Returns = defaultdict(float) # Change! this is SUM now
Q = defaultdict(float) # this didn't change either
else:
pi, C, Returns, Q = resume_dicts
for e in range(ep):
S0, A0 = env.sample_state_action()
if focus_S0 is not None: S0 = focus_S0
traj, T = generate_episode_ES(env, pi, S0, A0)
G = 0
for t in range(T-1,-1,-1):
St, _, _, At = traj[t] # (st, rew, done, act)
_, Rt_1, _, _ = traj[t+1]
G = gamma * G + Rt_1
# Change to every-visit MC to save computation
C[(St, At)] += 1
Returns[(St, At)] += G
Q[(St, At)] = Returns[(St, At)] / C[(St, At)]
pi[St] = np.argmax([Q[St,a] for a in range(env.nb_actions)])
if callback is not None:
callback(e, Q)
return Q, pi, (pi, C, Returns, Q)
Define callback functions
- trace is a long list np.arrays - each array is 4d with dims: [player_sum, dealer_card, has_ace, action]
In [10]:
trace = [] # track Q-Values during training, don't forget to clear between runs!
def convert_to_sum(Q):
# convert dict to 4d array
# dims are: [player_sum, dealer_card, has_ace, action]
res = np.zeros([10, 10, 2, 2])
for ps in range(12,22):
for dc in range(1, 11):
for ha in [0, 1]:
for act in [0, 1]:
res[ps-12, dc-1, ha, act] = Q[(ps, dc, bool(ha)), act]
return res
def callback(ep, Q):
if ep % 1000 == 0:
trace.append(convert_to_sum(Q)) # append Q-Array (not dict)
Import new fancy plotting function
In [11]:
from helpers_0503 import plot_Q_trace
Start new training session, this time with trace
In [12]:
# Option 1 - START NEW TRAINING
trace = []
Q, pi, resume = monte_carlo_ES_control_ext(env, ep=1000000, gamma=1.0, callback=callback)
# Option 2 - CONTINUE
# run this as many times as required until convergence
# Q, pi, resume = monte_carlo_ES_control_ext(env, ep=1000000, gamma=1.0, callback=callback, resume_dicts=resume)
Investigate progress
In [13]:
print('Training episodes so far: ', len(trace)*1000)
plot_blackjack(Q, pi)
# plot_Q_trace(trace, has_ace=0) # plot everything
plot_Q_trace(trace, has_ace=0, start_at=-1000) # plot last 1000000 episodes
Above plot shows how Q-Values develop over time, couple notes:
- $\color{blue}{\text{"Stick" is blue}}$, $\color{red}{\text{"HIT" is red}}$
- this plot corresponds in layout to "No Usable Ace" policy plot
- each small plot is history of Q-Values for that state
- for some states Q-Values for Stick/Hit diverge immediately and stay apart
- for some states, especially some states in the row Player Sum == 12, Q-Values are very close together
Save the plot when done
In [14]:
# plot_blackjack(Q, pi, save_path='assets/fig_0503.png')
Timing Tests¶
In [15]:
%timeit -r1 monte_carlo_ES_control(env, ep=10000, gamma=1.0)
%timeit -r1 monte_carlo_ES_control_ext(env, ep=10000, gamma=1.0)
In [16]:
%timeit -r1 monte_carlo_ES_control(env, ep=100000, gamma=1.0)
%timeit -r1 monte_carlo_ES_control_ext(env, ep=100000, gamma=1.0)
In [17]:
%timeit -r1 monte_carlo_ES_control(env, ep=1000000, gamma=1.0)
%timeit -r1 monte_carlo_ES_control_ext(env, ep=1000000, gamma=1.0)