$$ \huge{\underline{\textbf{ SARSA }}} $$

In [1]:
def sarsa(env, ep, gamma, alpha, eps):
"""Sarsa (on-policy TD control)
Params:
env - environment
ep - number of episodes to run
gamma - discount factor [0..1]
alpha - step size (0..1]
eps - epsilon-greedy param
"""
def policy(st, Q, eps):
if np.random.rand() > eps:
return argmax_rand([Q[st,a] for a in env.act_space])
else:
return np.random.choice(env.act_space)
Q = defaultdict(float) # default zero for all, terminal MUST be zero
for _ in range(ep):
S = env.reset()
A = policy(S, Q, eps)
while True:
S_, R, done = env.step(A)
A_ = policy(S_, Q, eps)
Q[S,A] = Q[S,A] + alpha * (R + gamma * Q[S_,A_] - Q[S,A])
S, A = S_, A_
if done: break
return Q
Helper functions:
In [2]:
def argmax_rand(arr):
# break ties randomly, np.argmax() always picks first max
return np.random.choice(np.flatnonzero(arr == np.max(arr)))
 |
 |
Solve Windy Gridworld¶
In [3]:
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
from helpers_0604 import plot_windy
Auxiliary code here: helpers_0604.py
Let's define environment - x, y convention is as per figure

In [4]:
class WindyGridworld:
def __init__(self):
self.act_space = [0, 1, 2, 3] # LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3
self.reset()
def reset(self):
self._x, self._y = 0, 3 # agent initial position
return (0, 3)
def step(self, action):
# actions: LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3
self._x, self._y = self.transition(self._x, self._y, action)
if self._x == 7 and self._y == 3: # GOAL reached
return (self._x, self._y), -1, True # observation, reward, done
return (self._x, self._y), -1, False # obs, rew, done
def transition(self, x, y, action):
"""Perform transition from [x,y] given action"""
if x in [3,4,5,8]: y += 1 # windy
if x in [6,7]: y += 2 # woo, very windy
if action == 0: x -= 1 # left
elif action == 1: y -= 1 # down
elif action == 2: x += 1 # right
elif action == 3: y += 1 # up
else: raise ValueError('Action must be in [0,1,2,3]')
x = np.clip(x, 0, 9) # x range is [0..9]
y = np.clip(y, 0, 6) # y range is [0..6]
return x, y
def get_path(self, Q):
x, y = 0, 3 # agent starting position
path = [(x, y)] # save starting position
for _ in range(100): # limit steps in case policy is loopy
A_star = np.argmax([Q[(x,y),a] for a in [0, 1, 2, 3]]) # pick best action
x, y = self.transition(x, y, A_star) # take one step
path.append((x,y)) # save to path
if x == 7 and y == 3: break # if goal: break
return path
Create environment
In [5]:
env = WindyGridworld()
Solve. Note that 10k episodes doesn't always find optimal policy.
In [14]:
Q = sarsa(env, 10000, gamma=1., alpha=.5, eps=.1)
Plot
In [15]:
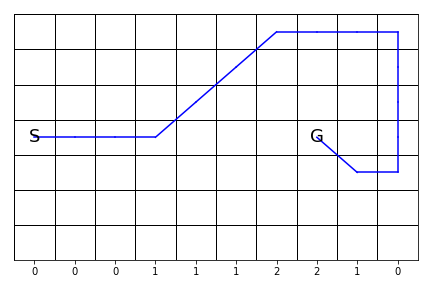
optimal_path = env.get_path(Q)
plot_windy(Q, optimal_path)
In [16]:
plot_windy(Q=None, path=optimal_path, saveimg=None) # 'assets/fig_0604a.png'
Episodes Figure¶
First, we need to extend sarsa so we can keep track which episode we are in on each time step. We also want to be able to limit number of timesteps.
In [17]:
def sarsa_ext(env, ep, gamma, alpha, eps, max_time_steps=None):
def policy(st, Q, eps):
if np.random.rand() > eps:
return argmax_rand([Q[st,a] for a in env.act_space])
else:
return np.random.choice(env.act_space)
hist_ep = [] # current episode nb saved on each time step
Q = defaultdict(float) # default zero for all, terminal MUST be zero
for current_episode in range(ep):
S = env.reset()
A = policy(S, Q, eps)
while True:
S_, R, done = env.step(A)
A_ = policy(S_, Q, eps)
Q[S,A] = Q[S,A] + alpha * (R + gamma * Q[S_,A_] - Q[S,A])
S, A = S_, A_
# Change! keep track of episode number history
hist_ep.append(current_episode)
if max_time_steps is not None:
if len(hist_ep) >= max_time_steps:
return Q, hist_ep
if done: break
return Q, hist_ep
Repeat experiment
In [18]:
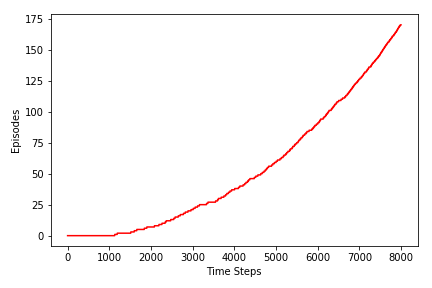
Q, hist_ep = sarsa_ext(env, 10000, gamma=1., alpha=.5, eps=.1, max_time_steps=8000)
And plot figure
In [19]:
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(hist_ep, color='red')
ax.set_xlabel('Time Steps')
ax.set_ylabel('Episodes')
plt.tight_layout()
plt.savefig('assets/fig_0604b.png')
plt.show()