$$ \huge{\underline{\textbf{ Gradient Monte Carlo }}} $$

Implementation below matches the box exactly, but is for educational purposes only. See notes.
Notes:
- function approximator should be implemented as independent object - passing vector w around is impractical in actual program
- I'm not sure why time step loop iterates foward (t=0,1..,T-1) instead of backwards (t=T-1,T-2,..,0), like we did in previous chapters (backward implementation is more efficient and avoids ackward Gt computation every time step)
- algorithm in the box is for undiscounted case and thus omnits $\gamma$ parameter
- For alternative implementation, which fixes above issues, see further below.
def gradient_MC(env, policy, ep, alpha, init_w, v_hat, grad_v_hat):
"""Gradient Monte Carlo Algorithm
Params:
env - environment
policy - function in a form: policy(state)->action
ep - number of episodes to run
alpha - step size (0..1]
init_w - function if form init_w() -> weights
v_hat - function in form v_hat(state, weights) -> float
grad_v_hat - function in form grad_v_hat(state, weights) -> delta_weights
"""
w = init_w()
for _ in range(ep):
traj, T = generate_episode(env, policy)
for t in range(T):
St, _, _, _ = traj[t] # (st, rew, done, act)
Gt = sum([traj[i][1] for i in range(t+1, T+1)]) # <- this is inefficient
w = w + alpha * (Gt - v_hat(St, w)) * grad_v_hat(St, w)
return w
Helper functions:
def init_w():
return np.zeros(10) # weights for 10 groups
def v_hat(St, w):
group = (St-1) // 100 # [1-100, 101-200, ..., 901-1000] -> [0, 1, ..., 9]
return w[group]
def grad_v_hat(St, w):
grad = np.zeros_like(w)
grad[(St-1)//100] = 1
return grad
def generate_episode(env, policy):
"""Generete one complete episode.
Returns:
trajectory: list of tuples [(st, rew, done, act), (...), (...)],
where St can be e.g tuple of ints or anything really
T: index of terminal state, NOT length of trajectory
"""
trajectory = []
done = True
while True:
# === time step starts here ===
if done: St, Rt, done = env.reset(), None, False
else: St, Rt, done = env.step(At)
At = policy(St)
trajectory.append((St, Rt, done, At))
if done: break
# === time step ends here ===
return trajectory, len(trajectory)-1
 |
Alternative Implementation¶
This section is very important, it is heavily built uppon in following chapters. We will reuse this implementation a lot later on. It's best to get good understanding right here, including both options 1 and 2 in the AggregateFunctApprox.
This implementation includes following features as compared with original implementation above:
- function approximator is now a trainable black-box object - can be tabular, linear, neural-net
- added discount paramter $\gamma$
- time-step loop now goes backward for efficiency
def gradient_MC_fix(env, policy, ep, gamma, model):
"""Gradient Monte Carlo Algorithm
Params:
env - environment
policy - function in a form: policy(state)->action
ep - number of episodes to run
gamma - discount factor [0..1]
model - function approximator, already initialised, with method:
train(state, target) -> None
"""
for _ in range(ep):
traj, T = generate_episode(env, policy)
Gt = 0
for t in range(T-1,-1,-1):
St, _, _, _ = traj[t] # (st, rew, done, act)
_, Rt_1, _, _ = traj[t+1]
Gt = gamma * Gt + Rt_1
model.train(St, Gt)
Aggregate Function Approximator
class AggregateFunctApprox():
"""Very simple function approximator"""
def __init__(self, learn_rate, nb_groups, group_size):
self._lr = learn_rate
self._group_size = group_size
self._w = np.zeros(nb_groups) # weights
def evaluate(self, state):
# Option 1:
group = (state-1) // self._group_size # [1-100, ..., 901-1000] -> [0, ..., 9]
return self._w[group] # return corresponding value
# Option 2:
# Implement as a special case of linear combination of features
# group = (state-1) // self._group_size # [1-100, ..., 901-1000] -> [0, ..., 9]
# x = np.zeros_like(self._w)
# x[group] = 1 # one-hot encoded feature vector [0, 1, 0]
# return x @ self._w # linear combination, i.e. dot product
def train(self, state, target):
# Option 1:
# Because grad_v_hat is a one-hot vector, we can optimize:
group = (state-1) // self._group_size
self._w[group] += self._lr * (target - self._w[group]) # update only one weight,
# standard MC update!
# Option 2:
# group = (state-1) // self._group_size
# x = np.zeros_like(self._w)
# x[group] = 1 # one-hot feature vector
# grad = x # grad. of lin. comb. is just x
Evaluate Example 9.1¶
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
Define environment
- V_approx values were picked by trial-and-error, they ignore both nonlinearity and terminal states (which should equal zero)
class LinearEnv:
"""
State nb: [ 0 1 ... 499 500 501 ... 1000 1001 ]
State type: [terminal . ... . start . ... . terminal]
"""
V_approx = np.arange(-1001, 1001, 2) / 1000.0 # ignore nonlinearity at terminal states
def __init__(self):
self.reset()
def reset(self):
self._state = 500
self._done = False
return self._state
def step(self, action):
if self._done: raise ValueError('Episode has terminated')
if action == 0: self._state -= np.random.randint(1, 101) # step left
elif action == 1: self._state += np.random.randint(1, 101) # step right
else: raise ValueError('Invalid action')
self._state = np.clip(self._state, 0, 1001) # clip to 0..1001
if self._state in [0, 1001]: # both 0 and 1001 are terminal
self._done = True
if self._state == 0:
return self._state, -1, self._done # state, rew, done
elif self._state == 1001:
return self._state, 1, self._done
else:
return self._state, 0, self._done
Plotting
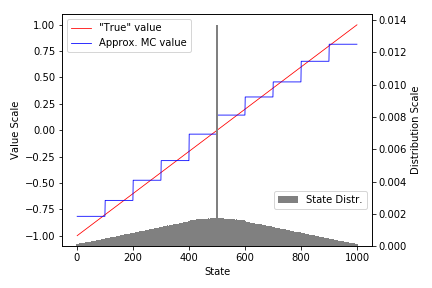
def plot_linear(V, env, freq=None, saveimg=None):
fig = plt.figure()
ax = fig.add_subplot(111)
# Note, state 0 is terminal, so we exclude it
ax.plot(range(1,1001), env.V_approx[1:], color='red', linewidth=0.8, label='"True" value')
ax.plot(range(1,1001), V[1:], color='blue', linewidth=0.8, label='Approx. MC value')
ax.set_xlabel('State')
ax.set_ylabel('Value Scale')
ax.legend()
if freq is not None:
mu = np.zeros(len(V)) # convert to array, V has same len as freq
for st in range(len(V)):
mu[st] = freq[st]
ax2 = ax.twinx()
# again, exclude terminal state 0
ax2.bar(range(1,1001), mu[1:], color='gray', width=5, label='State Distr.')
ax2.set_ylabel('Distribution Scale')
ax2.legend(loc='right', bbox_to_anchor=(1.0, 0.2))
plt.tight_layout()
if saveimg is not None:
plt.savefig(saveimg)
plt.show()
Create environment
env = LinearEnv()
Random policy
def policy(st):
return np.random.choice([0, 1])
Solve with original algorithm
weights = gradient_MC(env, policy, ep=10000, alpha=0.0003,
init_w=init_w, v_hat=v_hat, grad_v_hat=grad_v_hat)
V = [v_hat(st, weights) for st in range(1001)]
plot_linear(V, env)
Solve with proper function approximator
model = AggregateFunctApprox(learn_rate=0.0003, nb_groups=10, group_size=100)
gradient_MC_fix(env, policy, ep=5000, gamma=1.0, model=model)
V = [model.evaluate(st) for st in range(1001)]
plot_linear(V, env)
Recreate Figure 9.1¶
We need to track frequency of visit to each state, let's modify our algorithm slightly. Changes are marked with arrows.
def gradient_MC_track_freq(env, policy, ep, gamma, model):
count = defaultdict(float) # <- how many times state visited
total = 0 # <- total state visits to all states
for _ in range(ep):
traj, T = generate_episode(env, policy)
Gt = 0
for t in range(T-1,-1,-1):
St, _, _, _ = traj[t] # (st, rew, done, act)
_, Rt_1, _, _ = traj[t+1]
count[St] += 1
total += 1
Gt = gamma * Gt + Rt_1
model.train(St, Gt)
for key, val in count.items(): # <- calc. frequency
count[key] = val / total
return count # <- return freq.
Solve.
- In the book alg. is run for 100k episodes, alpha=2e-5. Here we run for 10k episodes alpha=1e-4 to save time.
model = AggregateFunctApprox(learn_rate=0.00001, nb_groups=10, group_size=100) # +10min?
freq = gradient_MC_track_freq(env, policy, ep=100000, gamma=1.0, model=model)
Plot
V = [model.evaluate(st) for st in range(1001)]
plot_linear(V, env, freq=freq, saveimg=None) # 'assets/fig_0901.png'