$$ \huge{\underline{\textbf{ Semi-Gradient TD }}} $$

Implementation below matches the box exactly, but is for educational purposes only. Function approximator should be implemented as independent object - passing vector w around is impractical in actual program
def semi_gradient_TD(env, policy, ep, gamma, alpha, init_w, v_hat, grad_v_hat):
"""Semi-Gradient TD Algorithm
Params:
env - environment
policy - function in a form: policy(state)->action
ep - number of episodes to run
gamma - discount [0..1]
alpha - step size (0..1]
init_w - function if form init_w() -> weights
v_hat - function in form v_hat(state, weights) -> float
grad_v_hat - function in form grad_v_hat(state, weights) -> delta_weights
"""
w = init_w()
for _ in range(ep):
S = env.reset()
while True:
A = policy(S)
S_, R, done = env.step(A)
w = w + alpha * (R + gamma * v_hat(S_, w) - v_hat(S, w)) * grad_v_hat(S, w)
S = S_
if done: break
return w
Helper functions:
def init_w():
return np.zeros(10) # weights for 10 groups
def v_hat(St, w):
if St in [0, 1001]: return 0 # return zero for terminal states
group = (St-1) // 100 # [1-100, 101-200, ..., 901-1000] -> [0, 1, ..., 9]
return w[group]
def grad_v_hat(St, w):
grad = np.zeros_like(w)
grad[(St-1)//100] = 1 # St=[1-100, ..., 901-1000] -> [0, ..., 9]
return grad
For TD prediction to work, V for terminal states must be equal to zero, always. Value of terminal states is zero because game is over and there is no more reward to get. Value of next-to-last state is reward for last transition only, and so on. If not, then bad things will happen.
 |
Alternative Implementation¶
Object oriented implementation that treats function approximator as a black-box trainable model.
def semi_gradient_TD_fix(env, policy, ep, gamma, model):
"""Semi-Gradient TD Algorithm
Params:
env - environment
policy - function in a form: policy(state)->action
ep - number of episodes to run
gamma - discount [0..1]
model - function approximator, already initialised, with method:
train(state, target) -> None
"""
for _ in range(ep):
S = env.reset()
while True:
A = policy(S)
S_, R, done = env.step(A)
model.train(S, R + gamma * model.evaluate(S_))
S = S_
if done: break
Function approximator
class AggregateFunctApprox():
"""Very simple function approximator"""
def __init__(self, learn_rate, nb_groups, group_size):
self._lr = learn_rate
self._nb_groups = nb_groups
self._group_size = group_size
self._w = np.zeros(nb_groups) # weights
def evaluate(self, state):
if state <= 0 or state > self._nb_groups * self._group_size:
return 0 # return zero for terminal states so TD works correctly
group = (state-1) // self._group_size # [1-100, ..., 901-1000] -> [0, ..., 9]
return self._w[group]
def train(self, state, target):
# Because grad_v_hat is a one-hot vector, we can optimize:
group = (state-1) // self._group_size # [1-100, ..., 901-1000] -> [0, ..., 9]
self._w[group] += self._lr * (target - self._w[group]) # standard TD update!
# Original impl., for reference:
# w = w + alpha * (R + gamma * v_hat(S_, w) - v_hat(S, w)) * grad_v_hat(S, w)
Evaluate Example 9.2 (left)¶
import numpy as np
import matplotlib.pyplot as plt
Define environment, same as in example 9.1
- V_approx values were picked by trial-and-error, they ignore both nonlinearity and terminal states (which should equal zero)
class LinearEnv:
"""
State nb: [ 0 1 ... 499 500 501 ... 1000 1001 ]
State type: [terminal . ... . start . ... . terminal]
"""
V_approx = np.arange(-1001, 1001, 2) / 1000.0 # ignore nonlinearity at terminal states
def __init__(self):
self.reset()
def reset(self):
self._state = 500
self._done = False
return self._state
def step(self, action):
if self._done: raise ValueError('Episode has terminated')
if action == 0: self._state -= np.random.randint(1, 101) # step left
elif action == 1: self._state += np.random.randint(1, 101) # step right
else: raise ValueError('Invalid action')
self._state = np.clip(self._state, 0, 1001) # clip to 0..1001
if self._state in [0, 1001]: # both 0 and 1001 are terminal
self._done = True
if self._state == 0:
return self._state, -1, self._done # state, rew, done
elif self._state == 1001:
return self._state, 1, self._done
else:
return self._state, 0, self._done
Plotting
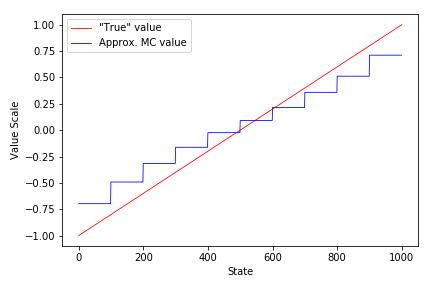
def plot_linear(V, env, freq=None, saveimg=None):
fig = plt.figure()
ax = fig.add_subplot(111)
# Note, state 0 is terminal, so we exclude it
ax.plot(range(1,1001), env.V_approx[1:], color='red', linewidth=0.8, label='"True" value')
ax.plot(range(1,1001), V[1:], color='blue', linewidth=0.8, label='Approx. MC value')
ax.set_xlabel('State')
ax.set_ylabel('Value Scale')
ax.legend()
plt.tight_layout()
if saveimg is not None:
plt.savefig(saveimg)
plt.show()
Create environment
env = LinearEnv()
Random policy
def policy(st):
return np.random.choice([0, 1])
Solve using original algorithm
weights = semi_gradient_TD(env, policy, ep=1000, gamma=1., alpha=0.1,
init_w=init_w, v_hat=v_hat, grad_v_hat=grad_v_hat)
V = [v_hat(st, weights) for st in range(0,1001)]
plot_linear(V, env)
Solve using function approximator
model = AggregateFunctApprox(learn_rate=0.1, nb_groups=10, group_size=100)
semi_gradient_TD_fix(env, policy, ep=1000, gamma=1.0, model=model)
V = [model.evaluate(st) for st in range(1001)]
plot_linear(V, env)
Recreate Figure 9.2 (left)¶
weights = semi_gradient_TD(env, policy, ep=10000, gamma=1., alpha=0.001,
init_w=init_w, v_hat=v_hat, grad_v_hat=grad_v_hat)
V = [v_hat(st, weights) for st in range(1001)]
plot_linear(V, env, saveimg=None) # 'assets/fig_0903b'