$$ \huge{\underline{\textbf{ Episodic Semi-Gradient Sarsa }}} $$

Differences from the box (see chapter 9.3 for explicit implementation example):
- $\hat{q}$ is a black box trainable function approximator, benefits:
- avoid explicitly passing around $\mathbf{w}$ - which can be quite complicated structure in some cases (e.g. neural net)
- avoid computing and stroing $\nabla\hat{q}(S,A,\mathbf{w})$ explicitly - which also can be complicated structure
- don't initialize $\mathbf{w}$ - one we don't know structure of $\mathbf{w}$, two maybe user want's to continue training
- add callback and trace params, so we can track what is going on
In [1]:
def ep_semi_grad_sarsa(env, ep, gamma, eps, q_hat, callback=None, trace=None):
"""Episodic Semi-Gradient Sarsa
Params:
env - environment
ep - number of episodes to run
gamma - discount factor [0..1]
eps - epsilon-greedy param
q_hat - function approximator, already initialised, with methods:
eval(state, action) -> float
train(state, target) -> None
"""
def policy(st, q_hat, eps):
if np.random.rand() > eps:
q_values = [q_hat.eval(st,a) for a in env.act_space]
return argmax_rand(q_values)
else:
return np.random.choice(env.act_space)
# skip weight intialization,
for e_ in range(ep):
S = env.reset()
A = policy(S, q_hat, eps)
for t_ in range(10**100):
S_, R, done = env.step(A)
if done:
q_hat.train(S, A, R)
break
A_ = policy(S_, q_hat, eps)
target = R + gamma * q_hat.eval(S_, A_)
q_hat.train(S, A, target)
S, A = S_, A_
if callback is not None:
callback(e_, t_, q_hat, trace)
Tile Coding - see chapter 9.5 for introduction
In [2]:
class TileCodingFuncApprox():
def __init__(self, st_low, st_high, nb_actions, learn_rate, num_tilings, init_val):
"""
Params:
st_low - state space low boundry in all dim, e.g. [-1.2, -0.07] for mountain car
st_high - state space high boundry in all dimensions
nb_actions - number of possible actions
learn_rate - step size, will be adjusted for nb_tilings automatically
num_tilings - tiling layers - should be power of 2 and at least 4*len(st_low)
init_val - initial state-action values
"""
assert len(st_low) == len(st_high)
self._n_dim = len(st_low)
self._lr = learn_rate / num_tilings
self._num_tilings = num_tilings
self._scales = self._num_tilings / (st_high - st_low)
# e.g. 8 tilings, 2d space, 3 actions
# nb_total_tiles = (8+1) * (8+1) * 8 * 3
nb_total_tiles = (num_tilings+1)**self._n_dim * num_tilings * nb_actions
self._iht = tiles3.IHT(nb_total_tiles)
self._weights = np.zeros(nb_total_tiles) + init_val / num_tilings
def eval(self, state, action):
assert len(state) == self._n_dim
assert np.isscalar(action)
scaled_state = np.multiply(self._scales, state) # scale state to map to tiles correctly
active_tiles = tiles3.tiles( # find active tiles
self._iht, self._num_tilings,
scaled_state, [action])
return np.sum(self._weights[active_tiles]) # pick correct weights and sum up
def train(self, state, action, target):
assert len(state) == self._n_dim
assert np.isscalar(action)
assert np.isscalar(target)
scaled_state = np.multiply(self._scales, state) # scale state to map to tiles correctly
active_tiles = tiles3.tiles( # find active tiles
self._iht, self._num_tilings,
scaled_state, [action])
value = np.sum(self._weights[active_tiles]) # q-value for state-action pair
delta = self._lr * (target - value) # grad is [0,1,0,0,..]
self._weights[active_tiles] += delta # ..so we pick active weights instead
Helper functions
In [3]:
def argmax_rand(arr):
# break ties randomly, np.argmax() always picks first max
return np.random.choice(np.flatnonzero(arr == np.max(arr)))
 |
Solve Mountain Car¶
Imports (source file: tiles3.py, helpers_1001.py)
In [4]:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from mpl_toolkits.mplot3d import axes3d
from mountain_car import MountainCarEnv
from helpers_1001 import eval_state_action_space, plot_q_max_3d
import tiles3 # by Richard Sutton, http://incompleteideas.net/tiles/tiles3.html
Environment
In [5]:
env = MountainCarEnv()
Create function approximator and solve
In [6]:
q_hat = TileCodingFuncApprox(env.state_low, env.state_high, len(env.act_space),
learn_rate=0.3, num_tilings=8, init_val=0)
ep_semi_grad_sarsa(env, ep=500, gamma=1.0, eps=0.0, q_hat=q_hat)
Plot
In [7]:
q_arr = eval_state_action_space(q_hat, env)
plot_q_max_3d(q_arr, env, labels=['Position', 'Velocity', ''], alpha=0.4)
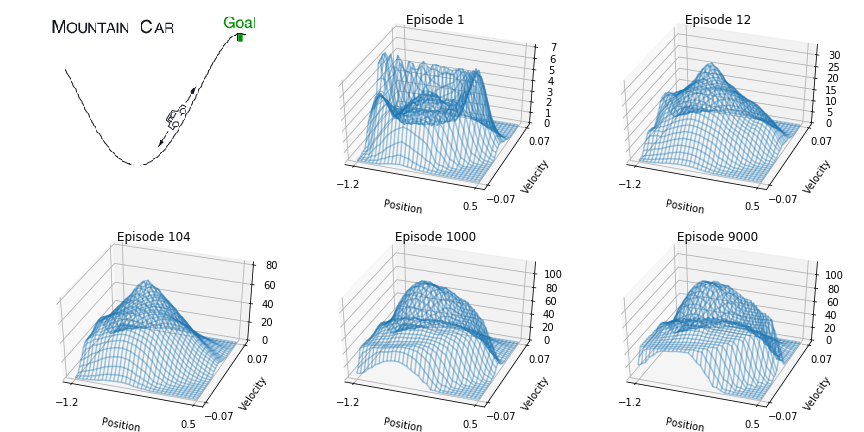
Recreate figure 10.1¶
We will need callback to capture q-value array for whole state-action space at specified episodes.
In [8]:
def callback(episode, tstep, model, trace):
"""Called from gradient_MC after every episode.
Params:
episode [int] - episode number
tstep [int] - timestep within episode
model [obj] - function approximator
trace [list] - list to write results to"""
episodes = [1, 12, 104, 1000, 9000]
if episode in episodes and tstep == 0:
q_arr = eval_state_action_space(q_hat, env)
trace.append(q_arr)
In [9]:
trace = []
q_hat = TileCodingFuncApprox(env.state_low, env.state_high, len(env.act_space),
learn_rate=0.3, num_tilings=8, init_val=0)
ep_semi_grad_sarsa(env, ep=20, gamma=1.0, eps=0.0, q_hat=q_hat, callback=callback, trace=trace)
In [289]:
fig = plt.figure(figsize=[12,6])
ax1 = fig.add_subplot(231)
ax2 = fig.add_subplot(232, projection='3d')
ax3 = fig.add_subplot(233, projection='3d')
ax4 = fig.add_subplot(234, projection='3d')
ax5 = fig.add_subplot(235, projection='3d')
ax6 = fig.add_subplot(236, projection='3d')
img = mpimg.imread('assets/1001_MountainCar_Image.png')
ax1.imshow(img)
ax1.axis('off')
labels = ['Position', 'Velocity', '']
plot_q_max_3d(trace[0], env, title='Episode 1', labels=labels, alpha=.4, axis=ax2)
plot_q_max_3d(trace[1], env, title='Episode 12', labels=labels, alpha=.4, axis=ax3)
plot_q_max_3d(trace[2], env, title='Episode 104', labels=labels, alpha=.4, axis=ax4)
plot_q_max_3d(trace[3], env, title='Episode 1000', labels=labels, alpha=.4, axis=ax5)
plot_q_max_3d(trace[4], env, title='Episode 9000', labels=labels, alpha=.4, axis=ax6)
plt.tight_layout()
plt.savefig('assets/fig_1001.png')
plt.show()