
Implementation of REINFORCE algorithm.
In [1]:
def REINFORCE(env, ep, gamma, alpha, init_theta=None):
"""REINFORCE algorithm.
Params:
env: OpenAI-like environment
ep (int): number of episodes to run
gamma (float): discount factor
alpha (float): learning rate
init_theta (np.array): initialize weights, default np.zeros()
"""
def policy(st, pi):
return np.random.choice(range(env.nb_actions), p=pi.pi(st))
hist_prob = []
hist_R = []
pi = TabularSoftmaxPolicyOptimized(lr=alpha, nb_states=env.nb_states,
nb_actions=env.nb_actions, init_theta=init_theta)
for e_ in range(ep):
# traj = [(st, rew, done, act), (st, rew, done, act), ...]
traj, T = generate_episode(env, policy, pi)
R_sum = traj[T][1]
for t in range(0, T):
St, Rt, _, At = traj[t] # (st, rew, done, act)
Gt = sum([gamma**(k-t-1) * traj[k][1] for k in range(t+1, T+1)])
pi.update(St, At, gamma**t * Gt)
R_sum += 0 if Rt is None else Rt
hist_prob.append(pi.pi(St))
hist_R.append(R_sum)
hist_prob = np.array(hist_prob)
hist_R = np.array(hist_R)
return hist_R, hist_prob
Helper functions:
In [2]:
def generate_episode(env, policy, *params):
"""Generete one complete episode.
Returns:
trajectory: list of tuples [(st, rew, done, act), (...), (...)],
where St can be e.g tuple of ints or anything really
T: index of terminal state, NOT length of trajectory
"""
trajectory = []
done = True
while True:
# === time step starts here ===
if done: St, Rt, done = env.reset(), None, False
else: St, Rt, done, _ = env.step(At)
At = policy(St, *params)
trajectory.append((St, Rt, done, At))
if done: break
# === time step ends here ===
return trajectory, len(trajectory)-1
 |
Setup¶
In [3]:
import numpy as np
import matplotlib.pyplot as plt
In [4]:
class CorridorSwitchedEnv:
"""Short corridor with switched actions. See example 13.1 in the book.
Note: Small change introduced to terminate after time step 1000
to prevent infinite loop if policy becomes deterministic.
"""
def __init__(self):
self.nb_states = 1
self.nb_actions = 2
self._state = 0
self._curr_iter = 0
def reset(self):
self._state = 0
self._curr_iter = 0
return 0 # states are indistinguisable
def step(self, action):
assert action in [0, 1] # left, right
if self._state == 0:
if action == 1:
self._state = 1
elif self._state == 1:
if action == 0: # left, swapped to right
self._state = 2
else: # right, swapped to left
self._state = 0
elif self._state == 2:
if action == 0:
self._state = 1
else:
self._state = 3 # terminal
else:
raise ValueError('Invalid state:', self._state)
# Terminate at time step = 1000
self._curr_iter += 1
if self._curr_iter >= 1000:
self._state = 3
if self._state == 3:
return 0, -1, True, None # obs, reward, done, extra
else:
return 0, -1, False, None
Policy Function¶
In [5]:
def softmax(x):
"""Numerically stable softmax"""
ex = np.exp(x - np.max(x))
return ex / np.sum(ex)
Implementation that matches book equations fairly closely
In [6]:
class TabularSoftmaxPolicyBook:
"""Tabular action-state function 'approximator'"""
def __init__(self, lr, nb_states, nb_actions, init_theta=None):
self._lr = lr # learning rate
self.n_st = nb_states
self.n_act = nb_actions
self._theta = np.zeros(nb_states * nb_actions) # weights
if init_theta is not None:
assert init_theta.dtype == np.float64
assert init_theta.shape == self._theta.shape
self._theta = init_theta
def x(self, state, action):
"""Construct feature vector, in our case just one-hot encode"""
xx = np.zeros(self.n_st * self.n_act) # construct x(s,a)
xx[state*self.n_act + action] = 1 # one-hot encode
return xx
def h(self, state, action):
"""Calculate preference h(s,a,theta), see e.q. 13.3"""
return self._theta @ self.x(state, action) # scalar
def pi(self, state):
"""Return policy, i.e. probability distribution over actions."""
# construct vector x(s,a) for each action
# perform full linear combination (e.q. 13.3)
h_vec = [self.h(state, b) for b in range(self.n_act)]
prob_vec = softmax(h_vec) # eq. 13.2
return prob_vec # shape=[n_act]
def update(self, state, action, disc_return):
# Option 1: as described in the book
prob_vec = self.pi(state) # shape=[n_act]
sum_b = [prob_vec[b]*self.x(state,b) # shape=[n_s*n_a]
for b in range(self.n_act)]
sum_b = np.sum(sum_b, axis=0)
grad_ln_pi = self.x(state, action) - sum_b # shape=[n_s*n_a], eq. 13.9
self._theta += self._lr * disc_return * grad_ln_pi # eq. 13.8
Equivalent implementation, simplified and optimized
In [7]:
class TabularSoftmaxPolicyOptimized:
"""Tabular action-state function 'approximator'"""
def __init__(self, lr, nb_states, nb_actions, init_theta=None):
self._lr = lr # learning rate
self.n_st = nb_states
self.n_act = nb_actions
self._theta = np.zeros(nb_states * nb_actions) # weights
if init_theta is not None:
assert init_theta.dtype == np.float64
assert init_theta.shape == self._theta.shape
self._theta = init_theta
def pi(self, state):
"""Return policy, i.e. probability distribution over actions."""
# Change 1:
h_vec = self._theta[state*self.n_act:state*self.n_act+self.n_act]
prob_vec = softmax(h_vec) # shape=[n_act], e.q. 13.2
return prob_vec
def update(self, state, action, disc_return):
x_s = np.zeros(self.n_act)
x_s[action] = 1 # feature vector, one-hot
prob = self.pi(state)
grad_s = x_s - prob
self._theta[state*self.n_act:state*self.n_act+self.n_act] += \
self._lr * disc_return * grad_s
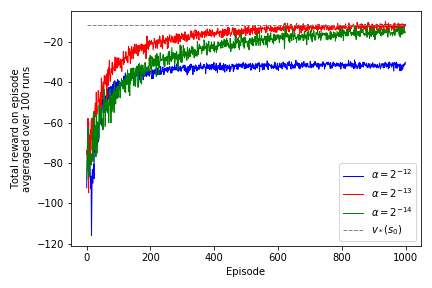
Recreate figure 13.1¶
We will use multiprocessing to speed things up (by a lot!)
In [8]:
import multiprocessing as mp
In [9]:
def run_single_experiment(alpha):
np.random.seed() # required due to multiprocessing
env = CorridorSwitchedEnv()
hist_R, _ = REINFORCE(env, ep=1000, gamma=1.0, alpha=alpha, init_theta=np.array([1.47, -1.47]))
return hist_R
In [10]:
def run_multiple_exp(repeat, param):
with mp.Pool(processes=mp.cpu_count()-2) as pool:
param_list = [(param,)] * repeat
results = pool.starmap(run_single_experiment, param_list)
results = np.array(results) # shape [nb_repeat, nb_episodes]
return np.average(results, axis=0) # shape [nb_episodes]
In [11]:
runs_a12_avg = run_multiple_exp(repeat=100, param=2**-12)
runs_a13_avg = run_multiple_exp(repeat=100, param=2**-13)
runs_a14_avg = run_multiple_exp(repeat=100, param=2**-14)
In [12]:
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(runs_a12_avg, linewidth=1.0, color='blue', label='$\\alpha = 2^{-12}$')
ax.plot(runs_a13_avg, linewidth=1.0, color='red', label='$\\alpha = 2^{-13}$')
ax.plot(runs_a14_avg, linewidth=1.0, color='green', label='$\\alpha = 2^{-14}$')
ax.plot([-11.6]*1000, linewidth=1.0, linestyle='--', color='gray', label='$v_*(s_0)$')
ax.set_ylabel('Total reward on episode\navgeraged over 100 runs')
ax.set_xlabel('Episode')
ax.legend()
plt.tight_layout()
plt.savefig('assets/fig_1301.png')
plt.show()