
In [1]:
import numpy as np
import matplotlib.pyplot as plt
Implementation of One-Step Actor-Critic
In [2]:
def one_step_actor_critic(env, ep, gamma, alpha_w, alpha_theta):
"""Sarsa (on-policy TD control)
Params:
env - environment
ep - number of episodes to run
gamma - discount factor [0..1]
alpha_w (float): learning rate for state-value function
alpha_theta (float): learning rate for policy
"""
def policy(st, pi):
return np.random.choice(range(env.nb_act), p=pi.pi(st))
hist_R = []
hist_val = []
hist_prob = []
v_hat = TabularStateValueFunction(lr=alpha_w, nb_states=env.nb_st)
pi = TabularSoftmaxPolicy(lr=alpha_theta, nb_states=env.nb_st, nb_actions=env.nb_act)
for _ in range(ep):
S = env.reset()
I = 1
R_sum = 0
while True:
A = policy(S, pi)
S_, R, done, _ = env.step(A)
target = R + gamma*v_hat.evaluate(S_) if not done else R
delta = target - v_hat.evaluate(S)
v_hat.train(S, target)
pi.update(S, A, I*delta)
I *= gamma
S = S_
R_sum += R
if done:
break
# Record metrics
hist_R.append(R_sum)
hist_val.append(v_hat.evaluate_all())
hist_prob.append(pi.pi_all())
hist_R = np.array(hist_R)
hist_val = np.array(hist_val)
hist_prob = np.array(hist_prob)
return hist_R, hist_val, hist_prob
Helpers
In [3]:
def softmax(x):
"""Numerically stable Softmax over last dimension"""
max_ = np.max(x, axis=-1, keepdims=True) # shape: (..., 1)
ex = np.exp(x - max_) # shape: (..., nb_act)
ex_sum = np.sum(ex, axis=-1, keepdims=True) # shape: (..., 1)
return ex / ex_sum # shape: (..., nb_act)
def test_softmax():
probabilities = [[0.1, 0.2, 0.3, 0.4],
[0.4, 0.3, 0.2, 0.1]]
logits = np.log(probabilities) # log is inverse of softmax
assert np.allclose(softmax(logits), probabilities)
print('PASS')
test_softmax()
In [4]:
class TabularStateValueFunction:
"""Tabular state-value function 'approximator'"""
def __init__(self, lr, nb_states):
assert isinstance(lr, float)
assert isinstance(nb_states, tuple)
self._lr = lr
self._w = np.zeros(nb_states)
def evaluate(self, state):
assert isinstance(state, (int, tuple))
assert self._w.ndim == 1 if isinstance(state, int) else len(state)
# or onehot(state, nb_states) @ self._w
return self._w[state]
def evaluate_all(self):
return self._w.copy()
def train(self, state, target):
assert isinstance(state, (int, tuple))
assert self._w.ndim == 1 if isinstance(state, int) else len(state)
assert isinstance(target, float)
value = self.evaluate(state)
self._w[state] += self._lr * (target - value)
def test_tsvf():
# Test 1D case, state is int
tsvf = TabularStateValueFunction(lr=0.1, nb_states=(2,))
tsvf.train(1, 1.0)
assert tsvf.evaluate(0) == 0.0
assert tsvf.evaluate(1) == 0.1
# Test 2D case, state is tuple
tsvf = TabularStateValueFunction(lr=0.1, nb_states=(2,2))
tsvf.train((0,1), 1.0)
tsvf.train((1,0), 2.0)
tsvf.train((1,1), 4.0)
assert tsvf.evaluate((0,0)) == 0.0
assert tsvf.evaluate((0,1)) == 0.1
assert tsvf.evaluate((1,0)) == 0.2
assert tsvf.evaluate((1,1)) == 0.4
print('PASS')
test_tsvf()
In [5]:
class TabularSoftmaxPolicy:
"""Tabular action-state function 'approximator'"""
def __init__(self, lr, nb_states, nb_actions, init_theta=None):
assert isinstance(lr, float)
assert isinstance(nb_states, tuple)
assert isinstance(nb_actions, int)
self._lr = lr # learning rate
self.n_act = nb_actions
self._theta = np.zeros((*nb_states, nb_actions)) # weights
if init_theta is not None:
assert init_theta.dtype == np.float64
assert init_theta.shape == self._theta.shape
self._theta = init_theta
def pi(self, state):
"""Return policy, i.e. probability distribution over actions."""
assert isinstance(state, (int, tuple))
assert self._theta.ndim == 2 if isinstance(state, int) else len(state)+1
h_vec = self._theta[state]
prob_vec = softmax(h_vec) # shape=[n_act], e.q. 13.2
assert prob_vec[0] != 0.0 and prob_vec[0] != 1.0
assert prob_vec[1] != 0.0 and prob_vec[1] != 1.0
assert prob_vec.ndim == 1
return prob_vec
def pi_all(self):
return softmax(self._theta)
def update(self, state, action, disc_return):
x_s = np.zeros(self.n_act)
x_s[action] = 1 # feature vector, one-hot
prob = self.pi(state)
grad_s = x_s - prob
self._theta[state] += self._lr * disc_return * grad_s
def test_tsp():
tsp = TabularSoftmaxPolicy(lr=0.1, nb_states=(2,), nb_actions=2)
tsp.update(state=1, action=0, disc_return=3.0)
tsp.update(state=1, action=1, disc_return=6.0)
assert np.allclose(tsp.pi(0), np.array([0.5, 0.5]))
assert np.allclose(tsp.pi(1), np.array([0.40387835, 0.59612165]))
tsp = TabularSoftmaxPolicy(lr=0.1, nb_states=(2,2), nb_actions=2)
tsp.update(state=(1,1), action=0, disc_return=3.0)
tsp.update(state=(1,1), action=1, disc_return=6.0)
assert np.allclose(tsp.pi((0,0)), np.array([0.5, 0.5]))
assert np.allclose(tsp.pi((1,1)), np.array([0.40387835, 0.59612165]))
print('PASS')
test_tsp()
 |
Setup¶
In [6]:
class LinearEnv:
"""
State Index: [ 0 1 2 3 4 5 6 ]
State Label: [ . A B C D E . ]
Type: [ T . . S . . T ]
"""
V_true = [0.0, 1/6, 2/6, 3/6, 4/6, 5/6, 0.0]
def __init__(self):
self.nb_st = (7,)
self.nb_act = 2
self.st_space = list(range(7))
self.act_space = [0, 1] # LEFT = 0, RIGHT = 1
self.reset()
def reset(self):
self._state = 1 # np.random.randint(1, 5+1)
self._done = False
return self._state
def step(self, action):
if self._done: raise ValueError('Episode has terminated')
if action not in [0, 1]: raise ValueError('Invalid action')
if action == 0: self._state -= 1
if action == 1: self._state += 1
reward = -0.1
if self._state < 1: self._done = True
if self._state > 5: self._done = True; reward = 1.0
return self._state, reward, self._done, None # obs, rew, done, debug
In [7]:
import matplotlib.patches as patches
In [8]:
class CliffWalkingEnv:
def __init__(self):
self.nb_st = (12, 4)
self.nb_act = 4
self.act_space = [0, 1, 2, 3] # LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3
self.reset()
def reset(self):
self._x, self._y = 0, 0 # agent initial position
return (0, 0)
def step(self, action):
"""actions: LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3"""
self._x, self._y = self.transition(self._x, self._y, action)
if self._x in range(1,11) and self._y == 0: # CLIFF spanning x=[1..10]
self._x, self._y = 0, 0 # teleport to start
return (self._x, self._y), -100.0, False, None # return -100 reward
if self._x == 11 and self._y == 0: # GOAL at (11,0)
return (self._x, self._y), -1.0, True, None # -1, terminate
return (self._x, self._y), -1.0, False, None # NORMAL states
def transition(self, x, y, action):
"""Perform transition from [x,y] given action. Does not teleport."""
if action == 0: x -= 1 # left
elif action == 1: y -= 1 # down
elif action == 2: x += 1 # right
elif action == 3: y += 1 # up
else: raise ValueError('Action must be in [0,1,2,3]')
x = np.clip(x, 0, 11) # x range is [0..11] incl.
y = np.clip(y, 0, 3) # y range is [0..3] incl.
return x, y
def get_path(self, P):
"""Returns a path agent would take, if following greedy Q-based policy"""
x, y = 0, 0 # agent starting position
path = [(x, y)] # save starting position
for _ in range(100): # limit steps in case policy is loopy
A_star = np.argmax(P[x, y]) # pick best action
x, y = self.transition(x, y, A_star) # take one step
path.append((x,y)) # save to path
if x in range(1,11) and y == 0: # CLIFF
path.append((0, 0)) # teleport
if x == 11 and y == 0: break # GOAL at (11,0)
return path
In [9]:
def plot_cliffwalk(P, paths, colors, labels, saveimg=None):
"""Plot windy gridworld."""
assert P is None or (P.shape[0] == 12 and P.shape[1] == 4)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_xlim(-.5, 11.5) # cliffwalk x range [0..11]
ax.set_ylim(-.5, 3.5) # y range [0..3]
ax.set_yticks([])
ax.set_xticks([])
ax.axis('off')
ax.set_aspect('equal', 'datalim')
# Start, Goal, The Cliff markers
params = {'horizontalalignment':'center', 'verticalalignment':'center'}
ax.text(0, 0, 'S', fontsize=18, **params)
ax.text(11, 0, 'G', fontsize=18, **params)
ax.text(5.5, 0, 'T h e C l i f f', fontsize=18, **params)
for x in range(12):
for y in range(4):
if x not in [0, 11] and y == 0: # cliff
ax.add_patch(patches.Rectangle([x-0.5, y-0.5], 1, 1, fill=True, color='lightgray'))
else:
ax.add_patch(patches.Rectangle([x-0.5, y-0.5], 1, 1, fill=False)) # cells
if P is not None:
params = {'head_width':0.2, 'head_length':0.2, 'color':'gray', 'alpha':.2}
A_star = np.argmax(P[x, y]) # pick best action
if A_star == 3: ax.arrow(x, y, 0, .1, **params) # up
elif A_star == 1: ax.arrow(x, y, 0, -.1, **params) # down
elif A_star == 0: ax.arrow(x, y, -.1, 0, **params) # left
elif A_star == 2: ax.arrow(x, y, .1, 0, **params) # right
def plot_path(path, color, label):
if path is not None:
for i in range(len(path)-1):
x, y = path[i]
x_, y_ = path[i+1]
if i == 0:
ax.plot([x, x_], [y, y_], color=color, alpha=1., label=label)
else:
ax.plot([x, x_], [y, y_], color=color, alpha=1.)
for path, color, label in zip(paths, colors, labels):
plot_path(path, color, label)
fig.legend(loc=4)
plt.tight_layout()
if saveimg is not None:
plt.savefig(saveimg)
plt.show()
Algorithms¶
SARSA¶
In [10]:
def argmax_rand(a):
"""Break ties randomly, (np.argmax always picks first max)."""
assert isinstance(a, list) or a.ndim == 1
return np.random.choice(np.flatnonzero(a == np.max(a)))
In [11]:
def Q_table_to_probabilities(Q, eps):
assert Q.ndim >= 2
state_shape = Q.shape[:-1]
nb_act = Q.shape[-1]
amax_flat = np.argmax(Q, axis=-1).flatten() # shape[prod(*nb_st)] 1D
one_hot = np.eye(nb_act)[amax_flat] # shape [prod(*nb_st), nb_act] 2D
probs = one_hot.reshape(*state_shape, -1) # shape [*nb_st, nb_act] ND
probs *= 1.0 - eps
probs += eps / Q.shape[-1]
assert probs.shape == Q.shape
assert np.all(probs.sum(axis=-1) == 1.0)
return probs
In [12]:
def sarsa(env, ep, gamma, alpha, eps):
"""Sarsa (on-policy TD control)
Params:
env - environment
ep - number of episodes to run
gamma - discount factor [0..1]
alpha - step size (0..1]
eps - epsilon-greedy param
"""
def policy(st, Q, eps):
if np.random.rand() > eps:
return argmax_rand(Q[st])
else:
return np.random.randint(env.nb_act)
hist_R = []
hist_Q = []
hist_P = []
Q = np.zeros((*env.nb_st, env.nb_act)) # default zero for all
N = np.zeros((*env.nb_st, env.nb_act))
for _ in range(ep):
S = env.reset()
A = policy(S, Q, eps)
R_sum = 0.0
while True:
S_, R, done, _ = env.step(A)
A_ = policy(S_, Q, eps)
Q_next = Q[S_][A_] if not done else 0.0
assert not done or Q_next == 0.0
Q[S][A] = Q[S][A] + alpha * (R + gamma * Q_next - Q[S][A])
N[S][A] += 1
S, A = S_, A_
R_sum += R
if done:
break
hist_R.append(R_sum)
hist_Q.append(Q.copy())
hist_P.append(Q_table_to_probabilities(Q, eps))
hist_R = np.array(hist_R)
hist_Q = np.array(hist_Q)
hist_P = np.array(hist_P)
return Q, N, hist_R, hist_Q, hist_P
Solve Linear Environment¶
In [13]:
env = LinearEnv()
One-Step Actor-Critic¶
In [14]:
hist_R, hist_val, hist_prob = one_step_actor_critic(env, ep=2000, gamma=1.0, alpha_w=2**-2, alpha_theta=2**-3)
print('Average reward during second half:', np.average(hist_R[-1000:]))
In [17]:
_, (axR, axV) = plt.subplots(ncols=2, figsize=(12,3))
axR.plot(hist_R)
axV.plot(hist_val)
plt.show()
_, axes = plt.subplots(ncols=5, figsize=(12,3))
for i, ax in enumerate(axes, start=1):
ax.plot(hist_prob[:,i])
plt.show()
SARSA¶
In [14]:
Q, N, hist_R, hist_Q, hist_prob = sarsa(env, 2000, gamma=1., alpha=.5, eps=.1)
hist_val = np.sum(hist_Q * hist_prob, axis=-1)
print('Average reward during second half:', np.average(hist_R[-1000:]))
In [15]:
_, (axR, axV) = plt.subplots(ncols=2, figsize=(12,3))
axR.plot(hist_R)
axV.plot(hist_val)
plt.show()
_, axes = plt.subplots(ncols=5, figsize=(12,3))
for i, ax in enumerate(axes, start=1):
ax.plot(hist_prob[:,i])
plt.show()
Solve CliffWalking¶
In [14]:
env = CliffWalkingEnv()
Plotting helper
In [22]:
def plot_hist_grid(hist_arr, title, y_lim):
nb_x, nb_y = hist_arr.shape[1], hist_arr.shape[2]
fig, axes = plt.subplots(ncols=nb_x, nrows=nb_y, figsize=(16,4))
for x in range(nb_x):
for y in range(nb_y):
ax = axes[nb_y-y-1, x]
ax.plot(hist_arr[:,x,y])
if y != 0:
ax.set_xticks([], [])
if x != 0:
ax.set_yticks([], [])
ax.set_ylim(y_lim)
fig.suptitle(title)
plt.show()
One-Step Actor-Critic¶
In [15]:
hist_R_ac, hist_V_ac, hist_P_ac = one_step_actor_critic(
env, ep=5000, gamma=1.0, alpha_w=2**-9, alpha_theta=2**-8)
In [21]:
path_ac = env.get_path(hist_P_ac[-1])
plot_cliffwalk(hist_P_ac[-1], paths=[path_ac], colors=['green'], labels=['Actor-Critic'])
In [23]:
plot_hist_grid(hist_V_ac, title='State Values', y_lim=(-20, 0))
In [24]:
plot_hist_grid(hist_P_ac, title='Action Probabilities (< blue, v orange, > green, ^ red)', y_lim=(0, 1))
SARSA¶
In [42]:
_, _, hist_R_sr, hist_Q_sr, hist_P_sr = sarsa(env, 5000, gamma=1., alpha=.5, eps=.1)
hist_V_sr = np.sum(hist_Q_sr * hist_P_sr, axis=-1)
In [43]:
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(hist_R_sr, color='blue', label='Sarsa', alpha=.9)
ax.plot(hist_R_ac, color='green', label='Actor-Critic', alpha=.9)
ax.set_ylim(-1000, 0)
ax.set_ylabel('Reward')
ax.set_xlabel('Episode')
plt.legend()
plt.show()
In [44]:
path_sr = env.get_path(hist_P_sr[-1])
plot_cliffwalk(hist_P_sr[-1], paths=[path_sr], colors=['blue'], labels=['Sarsa'])
In [45]:
plot_hist_grid(hist_V_sr, title='State Values', y_lim=(-20, 0))
In [46]:
plot_hist_grid(hist_P_sr, title='Action Probabilities (< blue, v orange, > green, ^ red)', y_lim=(0, 1))
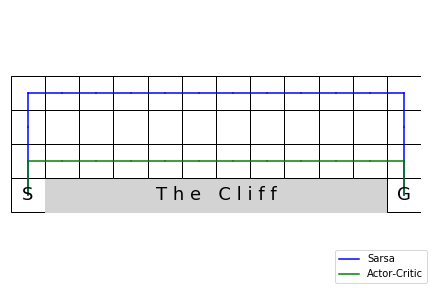
Compare Algorithms¶
In [54]:
plot_cliffwalk(None,
paths=[path_sr, path_ac],
colors=['blue', 'green'],
labels=['Sarsa', 'Actor-Critic'],
saveimg='assets/fig_one_step_actor_critic.png')